
Wiki
Anzapfung
Mit einer Anzapfung wird die Spannung eines Transformators bei einer bestimmten Windungszahl abgegriffen. Weil bei der A. eine andere Anzahl von Windungen in Reihe geschaltet ist, liegt eine andere Spannung an. Es besteht bei mehreren Anzapfungen, die sich in der Mitte der Wicklung befinden, auch die Möglichkeit Windungen zwischen zwei A. zu überbrücken.
Durch eine A. läßt sich also die Ausgangsspannung eines Transformators um einen bestimmten Prozentsatz verstellen. Dies kann z.B. nötig sein, um Spannungsschwankungen auszugleichen, wenn der Transformator mit wechselnder Last betrieben wird. Anzapfungen haben den Nachteil, daß wenn nur ein kleiner Anteil der Windungen verwendet wird, das Streufeld größer wird.
Man verwendet daher meistens Anzapfungen von maximal ± 5 - 10 %.
Siehe auch:
» StreufeldAußenleiterspannung, -strom
Eine Außenleiterspannung eines Transformators ist jede Spannung, die zwischen zwei Anschlußklemmen des Transformators abgegriffen werden kann. Ein Außenleiterstrom ist jeder Strom, der durch einen Anschluß in den Transformator fließt.
Weil die Außenleiterwerte sich auf das Verhalten eines Transformators nach außen hin beziehen, werden sie in einem Mehrphasensystem (wie z.B. Drehstrom) durch die Form der inneren elektrische Verkoppelung der einzelnen Phasen über die Wicklungsstränge mitbeeinflußt.
Siehe auch:
» Drehstrom » Strangspannung und -Strom » Bemessungsspannung » BemessungsstromBemessungsfrequenz
Ist die Betriebsfrequenz in Hz, für die der Transformator ausgelegt ist.
Bemessungsleistung
Die primär aufgenommene Scheinleistung eines Transformators in kVA oder MVA. Die Bemessungsleistung bildet die Grundlage für die Auslegung eines Transformators hinsichtlich der verbindlichen Angaben des Herstellers.
Siehe auch:
» ScheinleistungBemessungsspannung
Ist die Spannung, die sich zwischen den Klemmen eines leerlaufenden Transformators einstellt.
Die Spannung, die an den Klemmen einer beliebigen anderen Wicklung angelegt werden muß, damit sich diese Spannung einstellen kann, ist auch eine Bemessungsspannung. Jede Wicklung hat also ihre eigene Bemessungsspannung, die jeweils die Spannungserzeugungsformel, die eine Grundlage für die Konstruktion des Transformators ist, erfüllt.
Diese Spannung ist dem Typenschild des Transformators für jede Wicklung zu entnehmen. Im normalen Betriebsfall wird die primäre B. an der Primärwicklung angelegt, um an der Sekundärwicklung die dazugehörige sekundäre B. zu erhalten. Der Rückgang der Sekundärspannung unter Last wird mithilfe der Kurzschlußspannung uk berechnet.
Siehe auch:
» Kurzschlußspannung » Primär- und Sekundärseite » SpannungserzeugungsformelBemessungsstrom
Der Bemessungsstrom ist der Strom, der sich bei der Entnahme der Bemessungsleistung an einem Leiteranschluß des Transformators einstellt.
Siehe auch:
» BemessungsleistungBleche
Trafobleche müssen als Material des magnetischen Kreislaufs eines Transformators einen geringen magnetischen Widerstand mit einem hohen ohmschen Widerstand verbinden. Gleichzeitig sollten sie geringe Hystereseverluste haben.
Um diese Ziele zu erreichen werden Trafobleche kaltgewalzt, wodurch man eine Kornorientierung entlang der Vorzugsrichtung erreicht und damit eine höhere Permeabilität. Eine Isolationsbeschichtung der Bleche verhindert, dass sich Wirbelströme über mehrere Bleche hinweg bilden können.Wirbelströme innerhalb eines Bleches vermeidet man durch Legierung mit Silizium.
Als Ergebnis dieser Prozesse enstehen harte, spröde Bleche, die, in Rollen angeliefert, durch das Kernschneiden zu einem Transformatorkern verarbeitet werden können.
Im Gegensatz zu Kupfer, dessen elektrischer Widerstand bei Temperaturerhöhung ansteigt, fällt im Eisenkern der magnetische Widerstand bei Temperaturerhöhung leicht ab und die Hystereseverluste sinken. Das liegt daran, das infolge der stärkeren Wärmebewegung der Atome des Kernmaterials sich die Elementarmagnete im Eisens freier bewegen können.
Die von der ASA-Trafobau GmbH verwendeten Blechsorten sind ausschließlich kornorientiert und kaltgewalzt.
Siehe auch:
» Hystereseverluste » Permeabilität » VorzugsrichtungBlindleistung
Die Blindleistung wird mit dem Buchstaben Q bezeichnet und in var (Einheitenname: Var) gemessen. In vektorieller Darstellung bilden Blindleistung, Wirkleistung und Scheinleistung als skalare Größen entlang der hier dargestellten Zählpfeile immer ein rechtwinkliges Dreieck.
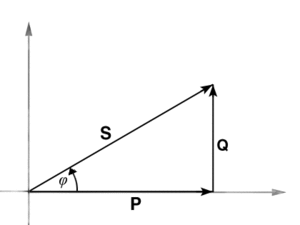
Bild B.1: Das S-P-Q Dreieck
Deshalb kann man nach dem Satz des Pythagoras aus zwei dieser Größen die dritte errechnen.
Die B. gibt das Produkt von 90° phasenversetzten Strömen und Spannungen an. Sie wird nach folgender Formel berechnet:![]()
Formel B.1: Die Blindleistung entspricht der auf die Hochachse projizierten Scheinleistung
Der Winkel φ entspricht dem Phasenversatz zwischen Spannung und Strom.
Die B. ist eigentlich keine Leistung, weil durch sie keine Energie nach außen gegeben wird (deshalb wird sie auch nicht in Watt gemessen). Sie ist eher eine Wechselbewegung von Energie zwischen den Energiespeicherelementen (Kondensator und Induktivität) des elektrischen Systems. Weil sich diese Energie auch durch die Anlagen und Leitungen des Netzes bewegt, müssen diese Bauteile für die Summe aus Blindleistung und Wirkleistung, die Scheinleistung, dimensioniert werden.
Bei dem Rechnen mit Blindleistung hat man folgende Möglichkeiten:
- Mit komplexen Widerständen Z rechnen und so positive ( Induktivität ) und negative (Kapazität) Blindleistungen erhalten, die man beliebig aufsummieren kann. Für φ kleiner Null entspricht die Formel oben einer Kapazität.
- Kapazitive und induktive Blindleistungen unterscheiden und für das Gesamtergebnis QC von QL abziehen. Dafür kann man dann φ und die Blindleistungen immer positiv sein lassen. Die Unterscheidung findet dann nicht mehr zwischen postiv und negativ sondern zwischen induktiv und kapazitiv statt. Die Zählpfeile der Blindleistungen in dem Diagramm zeigen in unterschiedliche Richtungen.
Die erste Möglichkeit ist deutlich eleganter, weil die Unterscheidung von kapazitiver und induktiver Blindleistung nur durch das Vorzeichen möglich ist und für beides das gleiche Formelzeichen verwendet werden kann. Es kann eine induktive Blindleistung in die selben Formeln eingestzt werden, wie eine kapazitive.
Bei der zweiten Möglichkeit vermeidet man die Entstehung negativer Ergebnisse durch Formeln mit Fallunterscheidung für bestimmte Frequenzen / Reaktanzen (z.B. unterschiedliche Formeln für die Kompensation von Induktivitäten / Kapazitäten).
Siehe auch:
» Wirkleistung » Scheinleistung » InduktivitätBuchholzrelais
Das B. ist eine Schutzeinrichtung für Öltransformatoren, die dazu dient im Fall eines Spannungsdurchschlags eine Warnmeldung zu geben, bzw. den Transformator sofort abzuschalten.
Es befindet sich beim Öltransformator an dem Verbindungsrohr zwischen dem Transformatorkessel und dem Ausdehnungstank.
Das B. funktioniert zunächst durch das Gas, das durch elektrolytische Zersetzung des Trafoöls bei einer Teilentladung entsteht. Die Gasblasen steigen nach oben und verdrängen das Öl aus einem Behälter innerhalb des B. . Dadurch sinkt ein Schwimmer und löst einen Quecksilberschalter aus. Dieser Mechanismus dient dazu, eine Warnmeldung bei einer relativ schwachen Entladung abzugeben.
Kommt es zu einem richtigen Lichtbogen, bildet sich durch die starke Wärmeausdehnung der Gasblase ein plötzlicher Ölschwall, der dann einen weiteren Quecksilberschalter über einen Stauschieber auslöst. Dieser Schalter nimmt den Transformator sofort vom Netz, um ihn vor einer weiteren Beschädigung zu schützen.
Drehstrom
In einem Drehstromnetz gibt es drei energieübertragende Leiter, deren Spannungen um 120° zueinander versetzt sind. Diese drei Spannungen sind ausreichend für die Erzeugung eines kreisförmig rotierenden Magnetfelds durch drei Elektromagnete oder können umgekehrt durch ein rotierendes Magnetfeld erzeugt werden.
Daher lassen sich mit Drehstrom sehr einfach elektrische Netze aufbauen, die von Drehstromgeneratoren gespeist werden und wo durch Drehstrommotoren mechanische Arbeit verrichtet wird. Dabei sind Generatoren und Motoren fast baugleich, weil sie nach dem selben Prinzip funktionieren. Die Vorteile der Drehstrommaschinen (keine Schleifkontakte, hoher Wirkungsgrad, gleichmäßiger Lauf) führten dazu, daß Drehstromnetze weit verbreitet sind.
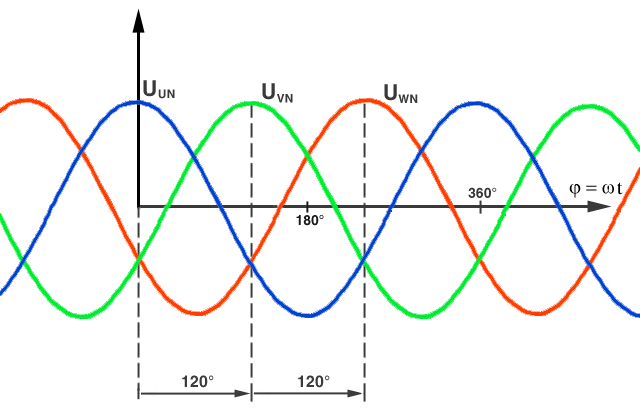
Bild D.1: Die Phasen des Drehstromnetzes als Liniendiagramm
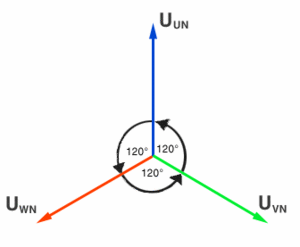
Bild D.2: Die Phasen des Drehstromnetzes als Zeigerdiagramm
Weil die Summe der Spannungen im Drehstromnetz immer gleich Null ist, hat sein Sternpunkt kein Potential gegenüber Erde; wenn die Belastung der einzelnen Phasen jedoch nicht symmetrisch ist, verschiebt sich das Potential des Sternpunkts vom Nullpunkt weg. Man spricht dann von einer Nullpunktverschiebung.
Durch Anschluß an den Neutralleiter kann der Sternpunkt auf Masse gezogen werden, wobei die Schieflast trotz verschwundener Nullpunktverschiebung vorhanden bleibt, aber eine andere Verteilung als vorher aufweist. Der Neutralleiter wird also belastet um das Potential des Sternpunkts auszugleichen. Die maximale Belastbarkeit und das Vorhandensein eines Neutralleiters hängt dabei von der Bauart und Schaltgruppe des Transformators ab.
Mit dem PE-Leiter zusammen hat man also fünf Leiter an einem Drehstromanschluß, wobei der Neutralleiter mit N und die Phasen nach der Phasenfolge mit L1, L2, L3 bezeichnet werden.
Die unterschiedlichen Möglichkeiten der Schaltung der drei Außenleiter an die Last führen zu verschiedenen Schaltgruppen. Eine weitere Unterscheidungsmöglichkeit besteht in dem Drehsinn eines Drehstromanschlusses. Weil man von vielen elektrischen Maschinen eine bestimmte Drehrichtung erwartet, muß häufig zur Sicherheit der Anschluß auf richtige Phasenfolge geprüft werden, obwohl diese eigentlich schon durch die Bezeichnung der Außenleiter und der Anschlüsse des Betriebsmittels vorgegeben ist. Durch Vertauschen zweier beliebiger Phasen kann die Drehrichtung dann gegebenenfalls umgekehrt werden.
Drehstromtransformator
Bei einem D. werden die einzelnen Phasen des Drehstromnetzes magnetisch durch den gemeinsamen Eisenkern verkoppelt. Man könnte auch einen D. aus drei entsprechend verschalteten Einphasentransformatoren (Drehstrombank) aufbauen, aber es ist effizienter das Kernmaterial für alle drei Phasen gleichzeitig zu benutzen. Weil für den magnetischen Fluß das Überlagerungsprinzip gilt, verhält sich der Transformator so, als ob die drei Phasen auf verschiedenen Eisenkernen angebracht wären.
Dieses Verhalten gilt aber nur für idealen Drehstrom; wenn auf Primär- oder Sekundärseite eine Schieflast anliegt, kann die Ausgangsspannung stark abfallen.
Aufbau eines typischen Drehstromtransfromators Schaltgruppe Dyn5
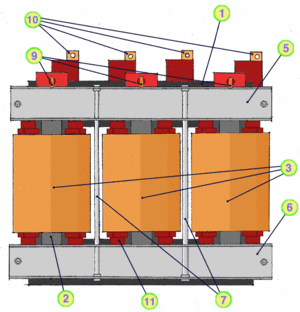
Bild D.4: Drehstromtransformator Dyn5: Oberspannungsseite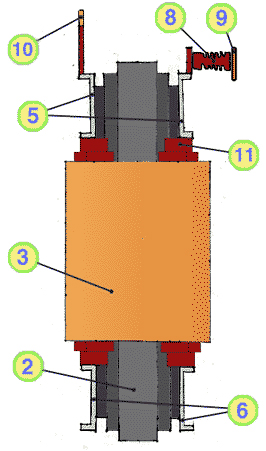
Bild D.5: Drehstromtransformator Dyn5: Seitenansicht
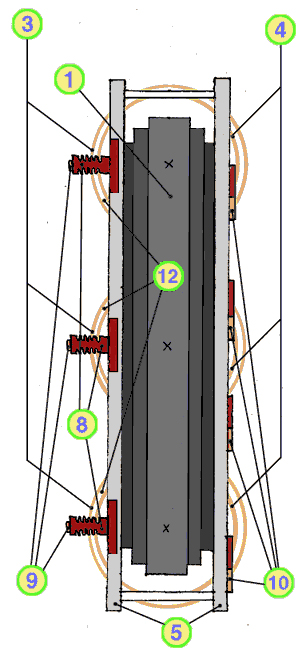
Bild D.6: Drehstromtransformator Dyn5: Ansicht von oben
- Joch des Kerns
- Schenkel des Kerns
- Oberspannungs - Wicklung
- Unterspannungs - Wicklung
- oberes Preßeisen
- unteres Preßeisen
- Zugstangen
- Oberspannungs - Stützer
- Anschlüsse Oberspannung:
U, V, W - Anschlüsse Unterspannung:
U, V, W, N - Abstützklötze
- Streukanal
Die mittlere Wicklung muß nicht so lange Feldlinien erzeugen. Deshalb ist der Leerlaufstrom dort nicht so groß wie an den beiden äußeren Wicklungen.
Außer der abgebildeten Dreischenkel - Bauweise gibt es noch Drehstromtransformatoren mit Fünfschenkelkern, die neben den äußeren Wicklungen noch zwei weitere Schenkel haben und mit einer geringeren Bauhöhe auskommen.
Bezeichnung der Anschlüsse eines Drehstromtransformators
Die Anschlußbezeichnung setzt sich aus drei Teilen zusammen:
- Wicklungsnummer:
Ziffer 1..3
Die Wicklungsnummer unterscheidet nicht die Wicklungsstränge unterschiedlicher Phasen, sondern die meistens galvanisch voneinander getrennten Wicklungen der gleichen Phase, die zusammen auf einem Schenkel des Transformators montiert sind. Üblich sind die Nummern 1 für Oberspannung und 2 für Unterspannung. - Leiteranschluß:
Welcher Leiter soll angeschlossen werden? Für Transformatoren gelten, wie für andere Betriebsmittel auch, die Anschlußbezeichnungen U, V, W, denen bei den Anschlußbezeichnungen des Netzes L1, L2, L3 gegenüberstehen:
U: Außenleiter L1
V: Außenleiter L2
W: Außenleiter L3
N: Neutralleiter - Position innerhalb des Wicklungsstrangs
1: Anfang
2: Ende
3 .. n: Anzapfung zwischen Anfang und Ende, gezählt vom Wicklungsstranganfang aus
Die unterschiedlichen Möglichkeiten die drei Phasen primär- und sekundärseitig zu verschalten werden unter dem Eintrag Schaltgruppen beschrieben.
Berechnung der Bemessungsleistung eines Drehstromtransformators
Bei der Berechnung der Bemessungsleistung aus der Bemessungspannung und dem Bemessungsstrom muß beachtet werden, daß die Spannung eine Außenleiterspannung darstellt und der Strom ein Außenleiterstrom des Transformators ist. Um nun die Bemessungsleistung des Transformators zu bestimmen muß man je nach Schaltgruppe die eine oder die andere dieser beiden Größen auf den entsprechenden Strangwert umrechnen (durch die Wurzel von 3 teilen) und dann das Ergebnis mal drei nehmen (drei Stränge im Drehstromtransformator). Die andere Größe kann so bleiben, weil sie schon dem entsprechenden Strangwert entspricht. Man kommt also immer auf folgendes Ergebnis:![]()
Formel D.1: Bemessungsleistung eines Drehstromtransformators
Siehe auch:
» Kern » Drehstrom » Feldlinien » Leerlaufstrom » Anzapfung » Bemessungsleistung » Bemessungsspannung » Bemessungsstrom » Außenleiterspannung, -stromDrossel
Eine Drossel begrenzt Ströme durch ihre Reaktanz. Zu diesem Zweck wird sie häufig in Reihe vor Verbraucher geschaltet, die einen sehr stark schwankenden Widerstand haben. Es kann dabei auch um die Glättung eines pulsierenden Stroms aus einer Stromquelle gehen.
Bei diesem Anwendungsgebiet spricht man von Glättungsdrosseln (bei der Anwendung auf Gleichstrom: "Gleichstromglättungsdrosseln"). Kommutierungsdrosseln werden in elektronischen Schaltungen als Energiespeicher benötigt.
Drosseln werden je nach Einsatzgebiet völlig unterschiedlich konstruiert, haben aber die gemeinsame Eigenschaft, das es sich um eine einfache Induktivität handelt, die meistens durch eine auf einem Eisenkern aufgebrachte Spule realisiert wird.
Daher kann man sie auch zur Kompensation von Blindlasten, die durch kapazitive Elemente hervorgerufen werden, benutzen. Man bezeichnet sie dann als Kompensationsdrossel. Eine solche Drossel kann auch die Verteilung der Blindleistung in einem Drehstromnetz symmetrieren (d.h. für gleiche Blindlast an allen drei Phasen sorgen). Daher kommt der Name Symmetrierdrossel, der in einem solchen Fall verwendet wird.
Damit sich eine Drossel in Bezug auf Linearität möglichst ähnlich zu einem ohmschen Widerstand verhält, werden meistens Luftspalte in den magnetischen Kreis eingebaut, wodurch der Einfluss der Hysteresekurve des Eisens gesenkt wird. Manchmal ist es sogar sinnvoll, ganz auf den Eisenkern zu verzichten und die Drossel als Luftspule auszulegen.
Eine Schwierigkeit bei der Konstruktion von Drosseln ist, die Erwärmung durch Kupferverluste gering zu halten, wenn sie z.B. in Reihe mit einem Verbraucher betrieben werden.
Dann baut man auch wassergekühlte Drosseln, bei denen das Kühlmittel innen durch den Leiter fließt.
Bei parallel geschalteten Kompensationsdrosseln sind geringe Eisenverluste wichtiger.
Siehe auch:
» Induktivität » Hysteresekurve » EisenverlusteDurchflutungssatz
Der D. beschreibt die Anordnung und Größe von Magnetfeldern relativ zur Lage und Stärke des felderzeugenden Stroms. In der hier angegebenen Form läßt er sich bei in der Energietechnik üblichen Frequenzen sowohl für gleichbleibende als auch für zeitlich veränderliche Felder anwenden.
Der D. besagt, daß jedes beliebige Umlaufintegral der magnetischen Erregung um eine stromdurchflossene Fläche genau dem Stromfluß durch diese Fläche entspricht.
Das Ergebnis dieses Umlaufintegrals ist eine magnetische Durchflutung , die nicht nur dieselbe Größe, sondern auch dieselbe Einheit (Ampere) wie die Stromstärke hat.
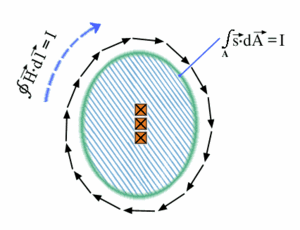
Bild D.7: Der Durchflutungssatz in grafischer Darstellung
Die Stromdichte s ist dabei ein Vektor, der in Richtung des Stromflusses zeigt (das ist in diesem Fall in die Bildebene hinein). Das die Fläche innerhalb des Umlaufintegrals viel größer als der eigentliche Stromleiter ist, spielt keine Rolle. Man kann die Teilflächen, in denen kein Strom fließt einfach ignorieren. Der Oberflächenvektor dA zeigt, wenn man sich entlang des Umlaufvektors dl bewegt senkrecht zur Fläche nach links.
Folgende Formel repräsentiert den D.: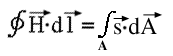
Formel D.2: Der Durchflutungssatz
Zusammen mit der Tatsache, daß für jeden Würfel der hineingehende Fluß gleich dem rausgehenden Fluß ist (Knotenpunktregel; Divergenz von Feldlinien = 0), bildet der Durchflutungssatz die Grundlage für die Berechnung magnetischer Kreise über Widerstandsnetzwerke. Im Unterschied zu dem Strom in Stromkreisen verläuft der magnetische Fluß auch im Vakuum und läßt sich daher nicht exakt auf bestimmte Leiterbahnen eingrenzen. Die genaue Berechnung von Magnetfeldern erfordert deshalb oft die numerische Bestimmung der räumlichen Feldverteilung, die einem sehr komplexen Widerstandsnetzwerk entspricht.
Der Durchflutungssatz ist in dem Sinn eine Analogie zu dem Kirchhoffschen Maschensatz für elektrische Netzwerke, daß die Summe der magnetischen Spannungen genau wie die Summe der elektrischen Spannungen im Stromkreis vorgegeben ist. Der Unterschied ist, daß in der obigen Darstellung des Modells des Magnetkreises die treibende Kraft nicht in dem Kreis sitzt sondern von ihm umschlossen wird. Man kann jedoch die Durchflutung bei der Berechnung von Magnetfeldern mittels eines magnetischen Widerstandsnetzwerks willkürlich an einer bestimmten Stelle in den Magnetkreis als Spannungsquelle einsetzen, vorausgesetzt man beachtet dabei die Verzweigungen, die auftreten.
Dieser Unterschied gegenüber elektrischen Widerstandsnetzwerken liegt also nur in der Betrachtungsweise, die bei Magnetfeldern stark von der räumlichen Feldverteilung geprägt ist und bei ohmschen Netzwerken durch die Aufteilung in unterschiedliche Bauelemente und fest vorgegebene Leiterbahnen bestimmt wird.
Aus den oben beschriebenen Gesetzen folgt, daß sich bei vorgebener Anordnung des Stromleiters über den spezifischen magnetischen Leitwert des Materials, der auch Permeabilität genannt wird, die Flußdichte an jeder Stelle im Raum bestimmen läßt. Das erreicht man bei einem geradlinig in einem homogenen Medium verlaufenden, unendlich langen Stromleiter durch ein kreisförmiges Umlaufintegral, von dem man wegen der Konstanz des Produkts in dem Integral leicht den Betrag der magnetischen Erregung in einer bestimmten Entfernung berechnen kann. Man teilt dazu durch den Umfang des Kreises 2? r und erhält die magnetische Erregung bzw. durch Multiplizieren mit der Permeabilität µ0 µr die magnetische Flußdichte.
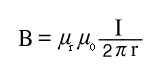
Formel D.3: Flußdichte im Abstand r von einem Leiter mit Strom I
Wenn man den Durchflutungssatz dazu verwendet, um die Verteilung magnetischer Spannungen in einer elektrischen Maschine zu berechnen, muß man beachten, daß sich die ferromagnetischen Abschnitte in dem Kreis wegen der von der Flußdichte abhängigen Permeabilität nichtlinear verhalten. D.h. man kann nur über eine iterative Berechnung auf die Spannungsverteilung kommen; eine Betrachtung als ohmsches Widerstandsnetzwerk reicht nicht aus.
Siehe auch:
» Magnetische Erregung H » Magnetische Durchflutung Θ » Feldlinien » Permeabilität » Magnetische Flußdichte » HysteresekurveDurchschlagsfestigkeit
Die Durchschlagsfestigkeit eines Isolierstoffs bezeichnet die elektrische Feldstärke, bei der ein plötzlicher Stromfluss einsetzt, weil stark beschleunigte Elektronen den Stoff ionisieren und durchschlagen. Sie wird mit Ed abgekürzt.
Die D. des Isolationsmediums eines Transformators ist mitbestimmend für seine Baugrösse, Lebensdauer und Belastbarkeit.
Bei Trockentransformatoren wird, neben den festen Isolierstoffen der Leiter, Luft als Isolation verwendet. Ihre D. ist abhängig von der Luftfeuchtigkeit und dem Luftdruck. Sie ist außerdem abhängig vom Abstand der Elektroden, bei grösseren Abständen sinkt sie. Deshalb kann man nicht immer dieselbe Feldstärke Ed nehmen und sie mit dem Abstand multiplizieren um die zulässige Spannung zu ermitteln, sondern man muss zuerst anhand einer Tabelle die für den Abstand gültige D. feststellen. In Tabellenwerken wird häufig 1 cm als Abstand für die angegebene Ed (z.B. 21 kV/cm bei Luft) angenommen. Bei festen Isolierstoffen ist es sinnvoller 1 mm als Messtrecke zu wählen, weil bei Messungen im cm - Bereich die Spannung so hoch werden kann, dass es zu einem Überschlag um die Probe herum kommt.
Weil die aus einer angelegten Spannung resultierende maximale Feldstärke von der Form der Elektroden abhängt, reicht die Spannung alleine nicht aus um die Feldstärke zu bestimmen und in Bezug zu der D. zu setzen. Eine geringe Feldstärke bei hoher Spannung erreicht man am besten durch runde, glatte Oberflächen an den betreffenden Leitern. Spitze Ecken führen zu hohen Feldstärken und Glimmentladungen. Daraus kann sich dann leichter ein Lichtbogen bilden.
In Öltransformatoren kann die D. schon durch einen geringen Wasseranteil im Öl stark herabgesetzt werden. Hier spielen auch Teilentladungen eine Rolle, die die Eigenschaften des Öls verschlechtern.
Thermische Alterung ist bei der D. von Öl und festen Isolierstoffen ein wichtiger Aspekt. Sie begrenzt letztendlich die Lebensdauer eines Transformators. Wegen der Erwärmung während des Betriebs wird die D. der Isolation durch Depolymerisation (das Zerbrechen von Molkülketten) und Oxidation herabgesetzt. (siehe Isolierstoffklassen)
Durchschlagsfestigkeit einiger Isolierstoffe
| Stoff | Durchschlagsfestigkeit Ed [kV/mm] |
|---|---|
| Epoxidharz | 35 |
| Glimmer | 25-70 |
| Papier | 5 |
| Polyethylen | 70-100 |
| Porzellan | 35 |
| PVC | 20-35 |
Siehe auch:
» IsolierstoffklassenEinschaltstrom
Der Einschaltstrom eines Transformators bei dem primärseitigen Zuschalten an das Stromnetz kann kurzzeitig um ein Vielfaches höher sein als sein Bemessungsstrom.
Besonders dann, wenn der Einschaltzeitpunkt mit einem Nullpunkt der Wechselspannung zusammenfällt, steigt die magnetische Erregung H auf einen ungünstig hohen Wert an. Dem Trafo steht bei diesem Einschaltzeitpunkt nämlich eine ganze Halbwelle zur Verfügung um sich aufzumagnetisieren. Ein Teil dieser Halbwelle wird sonst für die Ummagnetisierung benötigt. So wird der Trafo aber in die Sättigung getrieben, was zu einem relativ hohen Strom führt (siehe Hysteresekurve).
Mit elektronischen Schaltern hat man die Gelegenheit den Einschaltzeitpunkt schaltungstechnisch so vorzugeben, daß dieser erhöhte Einschaltstrom nicht auftritt.
Konstruktiv läßt sich der Einschaltstrom begrenzen, indem die Primärwicklung außen angeordnet wird. Durch die Drosselwirkung des Streufelds wird dann der Eingangswiderstand des Systems nach unten und der Einschaltstrom nach oben begrenzt.
Siehe auch:
» Magnetische Erregung H » Hysteresekurve » StreufeldEisenverluste
Die Eisenverluste bezeichnen die Summe der Verlustleistung im Kern des Transformators. Diese Summe setzt sich aus den Hystereseverlusten und den Wirbelstromverlusten zusammen. Im Ersatzschaltbild werden die E. durch einen ohmschen Widerstand parallel zur Hauptinduktivität repräsentiert. Sie können durch Messung der Leerlaufverluste ermittelt werden, die fast genau mit den E. übereinstimmen.
Der Begriff "Ummagnetisierungsverluste" wird in der Literatur mit unterschiedlichen Bedeutungen verwendet. Manchmal wird er mit den Eisenverlusten gleichgesetzt und manchmal bezieht er sich nur auf die Hystereseverluste. Die Bezeichnung der Hystereseverluste mit Ummagnetisierungsverlusten ist dabei die bessere Verwendung dieses Begriffs.
Siehe auch:
» Hystereseverluste » Wirbelstromverluste » LeerlaufverlusteFeldlinien
Magnetische Feldlinien geben die magnetische Flußdichte B mit ihrer räumlichen Verteilung wieder. Weil diese Flußdichte eine ortsabhängige, gerichtete Größe ist, kann man eine Feldlinie aus vielen Richtungspfeilen der Flußdichte zusammensetzen, indem man immer wieder ein kleines Stück in der angezeigten Richtung geht und dann neu die Feldrichtung des erreichten Ortes ermittelt.
Das Ergebnis dieses Vorgangs bildet sich von selber aus, wenn man Eisenfeilspäne in ein Magnetfeld gibt. Die Feldlinien werden dann durch die Anordnung der Späne sichtbar.
Das ändert jedoch nichts daran, daß magnetische Feldlinien genau wie Höhenlinien auf einer Landkarte nur ein willkürlich festgelegtes Gedankenmodell sind. Das Magnetfeld ist nämlich stetig im Raum verteilt und konzentriert sich nicht auf bestimmte Linien.
Die ermittelten Feldlinien haben immer die Eigenschaft eine geschlossene Kurve zu bilden und sich gegenseitig nicht zu schneiden. Mathematisch gesehen handelt es sich bei dem Magnetfeld nämlich um ein Vektorfeld, das in allen Punkten die Divergenz 0 hat, d.h. es gibt keine magnetischen Quellen oder Senken in Form eines Monopols, auf den die Feldlinien strahlenförmig zulaufen.
Man stellt Feldlinien häufig so dar, daß ihre Anzahl pro Flächeneinheit einer bestimmten Schnittebene der dort herrschenden Flußdichte entspricht. So kann optisch die Stärke und Richtung des Magnetfelds wiedergeben werden.
Siehe auch:
» Magnetische FlußdichteFluss (magnetischer)
Der Fluß Φ ist ein Maß, das den Umfang eines Magnetfelds für eine bestimmte Querschnittsfläche wiedergibt. Der Fluß wird in der Einheit Weber (Wb) gemessen, die einem Vs entspricht. Die Ursache für den Fluß ist eine magnetische Durchflutung Θ, die durch den fließenden Strom verursacht wird. Außerdem ist er abhängig von der Permeabilität des Materials, das er durchquert.
Der Fluß durch eine Fläche wird immer durch Integrieren der Flußdichte in Richtung der Oberflächenormalen dA der Fläche errechnet.
D.h. der Fluß einer Fläche bezieht automatisch nur senkrechte Anteile des Magnetfelds mit ein. Das ist bei allen Formeln zu beachten, in denen er vorkommt. Durch folgende Formel werden diese Verhältnisse wiedergegeben: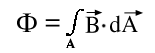
Formel M.5: Definition des magnetischen Flusses
Daher bezieht man sich, wenn man von einem magnetischen Fluß redet, oft unbewußt auf eine dazugehörige Fläche.
Bemerkenswert ist, daß der Fluß durch abgeschlossene Oberflächen von Körpern wie Würfel oder Kugeln immer 0 ist.
Für Bereiche mit konstanter Flußdichte in Richtung der Oberflächennormalen ergibt sich Φ = B *A
Das Induktionsgesetz erklärt den Zusammenhang zwischen zeitlicher Änderung des Flusses und induzierter Spannung.
Siehe auch:
» Feldlinien » Induktionsgesetz » Spannungserzeugungsformel » Permeabilität » Magnetische Durchflutung ΘFlussdichte B
Als magnetische Flußdichte, magnetische Induktion, magnetische Kraftflußdichte, oder in dem entsprechenden Kontext magnetische Polarisation J bezeichnet man die Dichte der Wirkung des Magnetfelds pro Flächeneinheit. In Formeln wird hierfür ein B verwendet.
Den Betrag dieser Größe kann man sich als abhängig von der Anzahl der Feldlinien pro Flächeneinheit vorstellen.![]()
Formel M.6: Magnetische Flußdichte in Abhängigkeit von magnetischer Erregung und Permeabilität
Die F. gibt aufgrund ihrer Vektornatur Aufschluß über die Stärke und Richtung der magnetischen Einwirkung auf einen bestimmten Ort. Sie wird in der Einheit Vs/m2 gemessen, die mit Tesla (T) bezeichnet wird. Früher war die Einheit ein Gauss, was 0,0001 Vs/m2 entspricht. Wenn man die F. über eine die Eisenquerschnittsfläche eines Transformators integriert bekommt man den wirkenden magnetischen Fluß als Ergebnis.
Siehe auch:
» Feldlinien » Permeabilität » Magnetischer Fluß ΦHysteresekurve
Die Hysteresekurve ist eine für jeden magnetischen Werkstoff spezifische Kennlinie, die die Beziehung von magnetischer Flußdichte B und magnetischer Erregung H im Verlauf eines Ummagnetisierungszyklus darstellt.
Ein Ummagnetisierungszyklus bedeutet stetiger Wechsel von H vom Maximum in eine Richtung zum Maximum in die entgegengesetzte Richtung und wieder zurück.
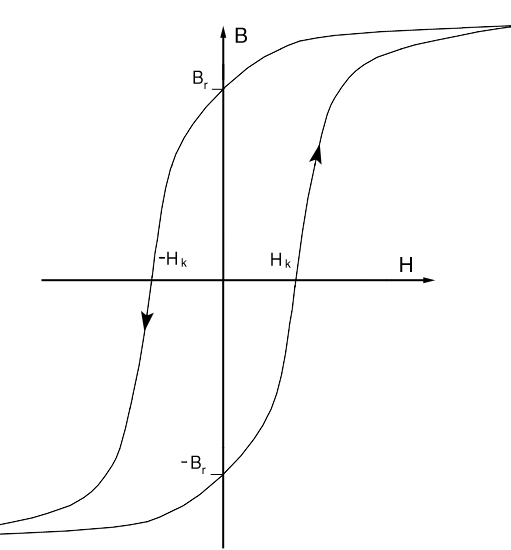
Bild H.1: Hysteresekurve
Man erkennt deutlich, dass wenn der Werkstoff in die Sättigung geht, die magnetische Erregung stark ansteigt, während sich die Flußdichte kaum ändert. Die H. ist mit Pfeilen gekennzeichnet, die angeben, in welcher Richtung sie durchlaufen wird. Die Flußdichte zu einer magnetischen Erregung lässt sich nur bestimmen, wenn bekannt ist ob der Werkstoff gerade aufmagnetisiert oder entmagnetisiert wird.
Man kann eine Neukurve einzeichnen, die den Vorgang des ersten Aufmagnetisierens vom Nullpunkt des Diagramms aus in eine bestimmte Richtung darstellt.
Das Bild zeigt, daß nach der magnetischen Sättigung, wenn der H - Wert wieder sinkt, die Flußdichte nicht so stark abnimmt, wie sie vorher gestiegen ist. Dieser Effekt ist auf die bleibende Ausrichtung der Elementarmagnete in einem ferromagnetischem Werkstoff zurückzuführen. Die Fläche, die sich so innerhalb der H. bildet, ist ein Maß für die Hystereseverluste.
Selbst wenn der Betrag der magnetische Erregung schon auf Null zurückgegangen ist, bleibt aufgrund dieses Effekts noch ein Flußdichte vorhanden. Sie wird als Remanenz Br bezeichnet und kann erst durch eine magnetische Erregung in die andere Richtung, die Koerzitivfeldstärke Hk , auf Null zurückgebracht werden.
Man unterscheidet nach der Form ihrer H. hartmagnetische und weichmagnetische Werkstoffe. Die hartmagnetischen haben eine sehr breite H., d.h. späte, meistens sehr plötzliche Übergänge zur Polarisation in die andere Richtung. Sie haben eine hohe Koerzitivfeldstärke. Weil sich einmal eingeprägte Felder so gut halten, werden diese Werkstoffe zur magnetischen Speicherung von Information verwendet. Die Fläche innerhalb H. ist bei ihnen groß, weshalb sie sich nicht für elektrische Maschinen eignen. Weichmagnetische Werkstoffe haben dagegen eine geringe Koerzitivfeldstärke. Dadurch werden die Fläche innerhalb der H. und damit die Eisenverluste geringer.
Es gibt auch eine andere Darstellungsform der H., bei der die durch eine Spule erzeugte magnetische Feldstärke H der Magnetisierungsfeldstärke M, die durch Polarisation des Materials ensteht, gegenübergestellt wird. Diese H. hat nach Erreichen der Sättigung im Gegensatz zu der hier abgebildeten keine bleibende Steigung µ0 mehr. Die bleibende Steigung entspricht dem üblichen Meßaufbau, wo Strom und integerierte Spannung an einer Spule als Eingangsgrößen für horizontale und vertikale Ablenkung eines Oszilloskops verwendet werden. Die Integration der Spannung kann über einen entsprechend beschalteten Operationsverstärker durchgeführt werden.
Den Zusammenhang zwischen Magnetisierung, Permeabilität und Suszeptibilität erklären die folgenden Formeln: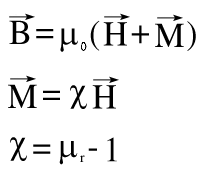
Formeln H.1: Magnetisierung M , relative Permeabilität µr und Suszeptibilität χ
Wobei für ferromagnetische Werkstoffe µr und χ im Verlauf der Kennlinie unterschiedliche Werte annehmen.
Bei der Erfassung einer H. sollte die Zeitverzögerung durch Nachlaufen der Flußdichte gegenüber der magnetischen Erregung keine Rolle spielen. Das heißt, bei dem Meßvorgang wird eine so geringe Frequenz gewählt, daß die Elementarmagnete sich viel schneller ausrichten, als sich das H - Feld ändert. Das bedeutet daß, wenn man an einem Punkt der Kurve anhalten würde (Stromfluß durch die Meßspule plötzlich gleichbleibend), der Meßwert in dem Diagramm auch nach beliebig langer Zeit nicht wegdriften würde.
Die Messung kann also mit einer beliebigen Wellenform durchgeführt werden, solange diese keine zu steilen Sprünge enthält (wie sie bei Rechteck- oder Sägezahnsignalen vorkommen).
Ein weiterer Grund für eine niedrige Meßfrequenz ist, das Meßergebnisse nicht durch von starken Flußdichteänderungen verursachten Wirbelstromverlusten verfälscht werden sollten.
Siehe auch:
» Flussdichte B » Magnetische Erregung H » Hystereseverluste » PermeabilitätHystereseverluste
Hytereseverluste enstehen durch die ständige Umpolung der Elementarmagnete in ferromagnetischen Werkstoffen im wechselnden Magnetfeld. Weil sich die Bereiche gleicher magnetischer Ausrichtung (die Weißschen Bezirke) bei Betragsänderung des Magnetfelds in Richtung Sättigung vergrössern, und dabei unter Aufwendung von Energie ihre Grenzwände neu finden müssen, setzen sie so die Energie des magnetischen Felds in Wärme um.
Die Menge der pro Volumeneinheit verlorenen Energie bei jedem Phasendurchlauf entspricht der Fläche innerhalb der Hysteresekurve. Aus der Formel der investierten elektrischen Energie kann man diese Beziehung über das Induktionsgesetz in Verbraucherschreibweise herleiten:
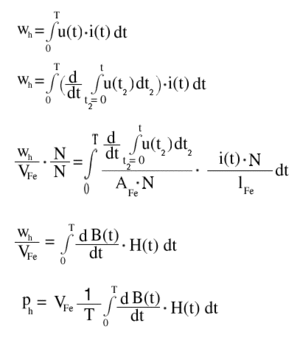
Formel H.2: Herleitung zur Bestimmung der Hystereseverluste
Die obenstehenden Formeln beziehen sich auf die skalaren Größen von B und H, deren Zählpfeile in die selbe Richtung zeigen.
N gibt die Anzahl der Windungen der Meßspule an.
T ist die Dauer einer Schwingunsperiode der Netzfrequenz (T = 1 / f)
VFe, lFe und AFe ergeben sich aus den Abmessungen des magnetischen Kreises:
AFe ist die Querschnittsfläche
lFe ist die mittlere Feldlinienlänge.
VFe = lFe AFe ist das Eisenvolumen, wobei man von einem vollständig mit Eisen gefüllten Kern ausgeht.
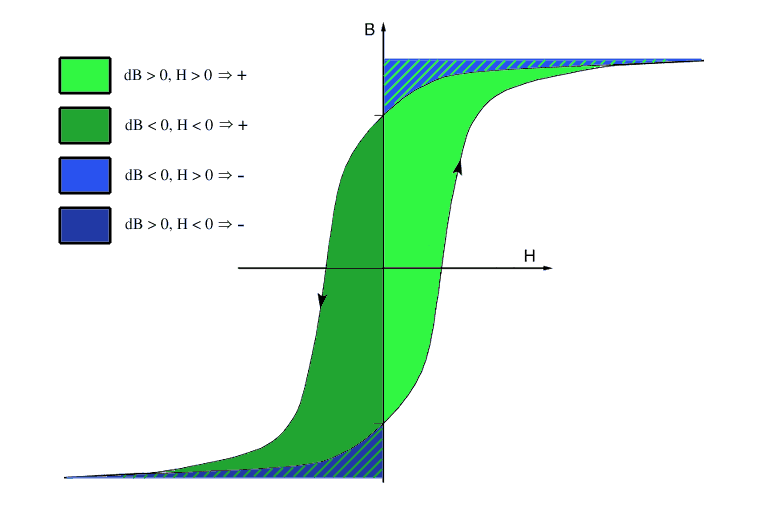
Bild H.2: Anschauliche Darstellung des Integrals
Das Bild zeigt eine grafische Darstellung des Integrals aus Formel H.2.
Die grünen Flächen in dem Bild tragen positiv zu dem Ergebnis bei, die grün - blau gestreiften Abschnitte repräsentieren Überlagerungen von positiven (grünen) und negativen (blauen) Teilflächen, die sich aufheben. Übrig bleibt also nur die Fläche innerhalb der Hysteresekurve.
Die Hystereseverlustleistung steigt daher linear mit der Frequenz und ungefähr quadratisch mit der Flußdichte.
Siehe auch:
» Hysteresekurve » Magnetische FlußdichteInduktion
Der Begriff "Induktion" bezeichnet:
- Eine Größe, die man auch magnetische Flußdichte nennt.
- Den Vorgang der Spannungserzeugung durch Änderung des magnetischen Flusses (Induktionsgesetz ). Die Spannung wird dann durch ein zirkulares elektrisches Feld hervorgerufen, das die Magnetfeldlinien in einer Ebene senkrecht dazu umschließt. Wenn sich in der Ebene dieses Feldes ein offener, kreisförmig gebogener, elektrischer Leiter befindet, kann man die induzierte Spannung an seinen Enden abgreifen. Ein induzierter Strom ensteht, wenn man die Leiterenden kurzschließt. Das Magnetfeld einer Spule wirkt bei Änderung des Stroms auf diese zurück und erzeugt eine Spannung, die der Stromänderung entgegenwirkt ( Lenzsche Regel ). Diesen Vorgang bezeichnet man als Selbstinduktion. Er ist Grundlage für die Energiespeicher - Wirkung der Induktivität. Die Induktion ist genau wie die Wirkung elektrischer Felder eine Fernwirkung, die auch das Vakuum durchquert und nicht nur an spezielle Leitermaterialien gebunden ist.
Siehe auch:
» Magnetische Flußdichte » Magnetischer Fluß Φ » Induktionsgesetz » Lenzsche Regel » InduktivitätInduktionsgesetz
Das Induktionsgesetz besagt, daß die in eine Leiterschleife induzierte Spannung gleich der zeitlichen Änderungsgeschwindigkeit des magnetischen Flusses, der durch sie hindurchgeht ist.
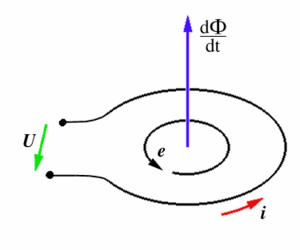
Bild I.1: Lage und Richtung der induzierten Größen und ihrer Ursache
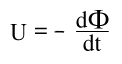
Formel I.1: Das Induktionsgesetz für Erzeugerzählpfeile
Das Vorzeichen in der Formel hängt vom gewählten Richtungssinn ab. Wenn man Verbraucherzählpfeile verwendet, sind die Leistungen U mal I, die man in das System hineinschickt positiv. Wenn man Erzeugerzählpfeile wie in der Abbildung verwendet, sind Leistungen, die aus dem System kommen positiv. Der eingetragene Stromzählpfeil entspricht dem mathematisch positiven Drehsinn, wobei die Größe des Stroms bei positiver Flußänderung in Zählpfeilrichtung negativ wäre. ( Rechte-Hand-Regel, Lenzsche Regel)
Die Formel bezieht sich gemäß Definition des magnetischen Flusses nur auf den Anteil des Magnetfelds, der senkrecht zur Spulenebene steht.
Wodurch die Änderung des magnetischen Flusses verursacht wird, ist egal. Die in dem Induktionsgesetz angegebene Spannung tritt in jedem Fall auf.
Einige der zahlreichen Möglichkeiten dieser Änderung sind Drehung einer Leiterschleife im Magnetfeld, Bewegung von außen in ein Feld hinein und wieder heraus, Austausch des Kernmaterials während der Strom fließt, Änderung des einwirkenden Feldes durch Stromänderung an der felderzeugenden Spule oder durch Annäherung eines Permanentmagneten, Längenänderung des magnetischen Kreises.
Daher gilt das I. für Elektromotoren, Generatoren, Transformatoren, Schaltnetzteile, Wirbelstrombremsen, Mikrophone, Fahrradtachos usw. Es ist also eine Grundlage für die Entwicklung aller elektrischer Maschinen.
Das I. lässt sich durch die Lorentzkraft bestätigen, wenn man sich eine offene rechteckige Drahtschleife in einem Magnetfeld vorstellt, die durch einen mit Schleifkontakten auf paralellen Leitern gleitenden Verbindungsdraht kontinuierlich vergrößert wird. Die Lorentzkraft des Magnetfelds auf die Elektronen in diesem bewegten Leiter verursacht dann eine Spannung, die genau der Spannung entspricht, die man auch durch das I. wegen der Flächen- und damit Flußänderung der Leiterschleife erhalten würde.
Bei den Transformatoren führt das I. zu der Spannungserzeugungsformel.
Genauso, wie man die Formel des I. umstellen kann, kann man auch den Wirkungszusammenhang umkehren, d.h. eine angelegte Spannung verursacht eine Änderung des magnetischen Flusses.
Die Grundlage des I. sind die Maxwellschen Gleichungen, die aber über den Rahmen dieses Lexikons hinausführen würden und in der Praxis für Transformatoren zu umständlich anzuwenden sind.
Siehe auch:
» Lenzsche Regel » Transformator » Lorentzkraft » SpannungserzeugungsformelInduktivität
"Induktivität" ist sowohl die Bezeichnung für eine elektrische Größe als auch der Name eines elektrischen Bauelements, das diese Größe als Eigenschaft hat (anders ist das bei "Kapazität" und "Kondensator").
Die I. als Größe gibt an, wieviel Spannung man wie lange wirken lassen muß, damit ein bestimmter Strom durch ein Bauelement fließt. Die Einheit der I. ist also Vs/A; der Einheitenname ist Henry (kurz: H, Formelzeichen L). Man kann sich diese Größe als die Trägheit des Stromflusses gegenüber Spannungen vorstellen, was auch durch die unten stehende Differentialgleichung wiedergegeben wird.
Eine I. als elektrisches Bauelement kann man daher als einen Speicher für Ströme bezeichnen, so wie man analog einen Kondensator als Speicher für Spannungen betrachten kann.
Die I. ist also ebenso wie der Kondensator ein Energiespeicher. Wenn eine I. und ein Kondensator sich in einer Schaltung gegenseitig beeinflussen, kann es zur Bildung von Schwingungen zwischen ihnen und zur Filterung bestimmter Frequenzen kommen.
Die Energie wird im Magnetfeld des magnetischen Kreises gespeichert und durch Induktion (die in diesem Fall als "Selbstinduktion" bezeichnet wird) zurück in den elektrischen Stromkreis übertragen.
Weil eine I. im zeitlichen Verhalten gegenüber Spannungen nicht neutral, sonder abhängig von ihrer Vergangenheit ist, reagiert sie auf sinusförmige Einflüsse unterschiedlicher Frequenz auch unterschiedlich. Dies wird durch die Formel des Widerstands wiedergegeben. Die Kreisfrequenz ? in dieser Formel entspricht 2?f, wobei f die Frequenz der anliegenden Spannung ist.
Formeln I.2: Alle wichtigen Formeln zur Induktivität im Überblick
Die letzte Formel bestimmt die Größe der Induktivität aus den geometrischen Daten des Bauelements:
Windungszahl N
Querschnittsfläche Amag
Länge des magnetischen Kreises lmag
Permeabilität µ0µr
Diese Formel hat ihren Ursprung im Induktionsgesetz und dem Durchflutungssatz.
Sie geht von idealen Bedingungen aus, die man in der Realität mit endlich langen Spulen nie erreicht :
Homogenes Magnetfeld über die gesamte Länge der Feldlinien
Magnetfeld nur innerhalb des Kerns
Permeabilität in alle Richtungen und bei allen magnetischen Feldstärken gleich.
Siehe auch:
» Induktion » Induktionsgesetz » Durchflutungssatz » Permeabilität » Magnetische Erregung HIsolierstoffklassen
Die I. teilen Isolierstoffe in Temperaturbereiche auf, für die sie geeignet sind. Die Isolierstoffe verlieren nämlich durch die ständig vorhandene Verlustwärme des Transformators an Wirkung. Dieser chemische Alterungsprozess wird mit steigender Temperatur exponentiell beschleunigt. Daher muss man Stoffe und Tränkmittel der entsprechenden Klasse verwenden, um eine ausreichende Lebensdauer der Isolierung zu erreichen.
Folgende Tabelle listet einige Isolierstoffe der wichtigsten Stoffklassen auf:
| Stoffklasse | Grenztemperatur | Isolierstoffe |
|---|---|---|
| A | 105°C | Baumwolle, Seide, Holz, Papier |
| E | 120°C | Polyesterharze, Drahtlacke |
| B | 130°C | Glasfaser, Drahtlacke, Glimmer, Epoxidharz |
| F | 155°C | Glasfaser, Drahtlacke, Polyamidfaser |
Kern
Der Kern eines Transformators hat die Aufgabe den magnetischen Kreis zu schließen und dabei möglichst den Wirkungsquerschnitt des magnetischen Feldes ganz auszufüllen. Der Trafokern ist meistens in Bleche aufgeteilt, die aus einem magnetischen Werkstoff bestehen. Man verwendet als Kernmaterial eine Eisenlegierung mit Silizium, um den elektrischen Widerstand zu erhöhen (Wirbelstromverluste). Dieses Material kann nach einem speziellen Verfahren kaltgewalzt werden, wodurch es eine magnetische Vorzugsrichtung bekommt.
Je größer ein Transformator ist, desto mehr wird sein Kernquerschnitt der Kreisform angenähert. Dies geschieht durch Abstufen des Kerns (Stufenkern). Kleine Transformatoren haben wegen der geringeren Herstellungskosten einen rechteckigen Kern. Auch die axiale Form des Kerns kann gegenüber dem rechteckigen Entwurfsmuster optimiert werden. Die rechteckige Bauweise hat nämlich den Nachteil, daß an den Übergängen der einzelnen Blechpakete Streufelder und erhöhte Eisenverluste enstehen.
Bei einem Schnittbandkern verlaufen die Feldlinien immer ungefähr in der Vorzugsrichtung des Materials, weil die Bleche an den Enden zueinander hin gebogen sind. Daraus resultiert ein hoher Wirkungsgrad wegen geringer Leerlaufverluste. Ein Ringkerntrafo hat aus diesem Grund einen torusförmigen Ferritkern, mit dem fertigungstechnischen Nachteil, daß die Wicklungen schwer auf den geschlossenen Kern aufzubringen sind.
Drehstrom - Trockentransformatorkerne werden gefertigt, indem zunächst die Bleche mit der Kernschneidemaschine zugeschnitten und in den richtigen Mengen abgezählt werden. Dann werden die Blechpakete im Joch und die Enden der Schenkel durch ein Preßeisen zusammengedrückt, um die Bleche im Kern möglichst dicht zu komprimieren. Am Ende der Fertigung werden die Joche durch Zugstangen aufeinander zu gezogen. Das ist nötig, weil schon ein sehr kleiner Luftspalt zwischen Schenkeln und Jochen eine deutliche Erhöhung des magnetischen Widerstands und damit des Leerlaufstroms verursacht.
Aufbau und Flußverteilung verschiedener Kernformen
1. Transformatoren für Drehstrom
1.1. Dreischenkelkerntransformator
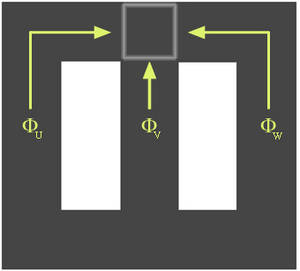
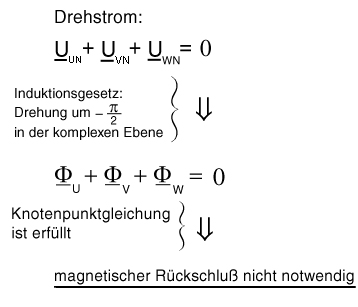
Bild K.1: Warum ein Drehstromtransformator mit drei Schenkeln auskommt
1.2. Fünfschenkelkerntransformator
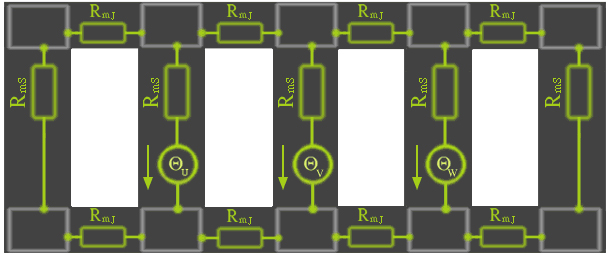
Bild K.2: Fünfschenkelkerntransformator als magnetisches Widerstandsnetzwerk mit drei Spannungsquellen
Das obige Widerstandsnetzwerk soll zeigen, daß ein vorhandener magnetischer Rückfluß doch beansprucht wird, wenn man ihn nicht in der Mitte, sondern an den äußeren Schenkeln anbringt. Dieses Widerstandsnetzwerk ist nicht für eine genaue Berechnung geeignet. Es dient nur dazu festzustellen, ob die zusätzlich angebrachten Schenkel etwas nützen.
Ein Fünfschenkelkerntransformator bringt hauptsächlich dann Vorteile, wenn man z.B. um einen großen Transformator per Bahn zu transportieren, eine geringe Bauhöhe beabsichtigt. Die äußeren Schenkel werden nur durchflossen, weil der magnetische Widerstand der Joche gegenüber dem der Schenkel nicht vernachlässigt werden kann. Das bedeutet, daß das Joch in der Mitte durch die äußeren Schenkel flußmäßig entlastet wird. Dadurch kann man an den Jochen oben und unten Bauhöhe sparen, wenn man sie für die gleiche Flußdichte wie die Schenkel auslegt.
2. Einphasen Transformatorkerne
2.1. Mantelkerntransformator
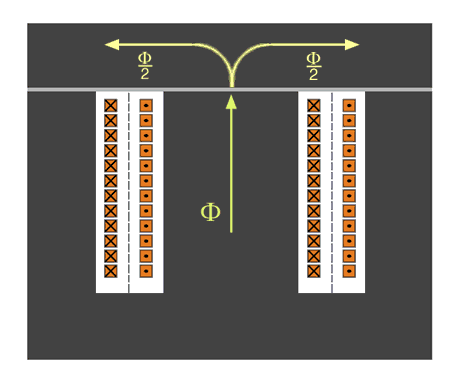
Bild K.3: Mantelkerntransformator (gestrichelte Linie ist Trennlinie zwischen Primär- und Sekundärseite)
Der Mantelkerntransformator ist die häufiger verwendete Bauart für kleine Einphasentransformatoren. Er ist kostengünstiger zu produzieren, weil er nur einen Spulenkörper hat. Seine Bauhöhe und sein Eisengewicht sind geringer als bei dem Kerntransformator.
Die beim Kleintrafobau für diesen Kerntyp verwendeten Bleche werden abfallos in einer nach dem Aussehen der Buchstaben als "EI" bezeichneten Form gestanzt. Das Joch wird dabei aus dem freiwerdenden Zwischenraum für die Wicklungen gewonnen. Aus der Form der Bleche wird ersichtlich, daß hier eine Verwendung von kornorientierten Material mit Vorzugsrichtung keinen Sinn macht und man auf dessen Vorteile verzichten muss.
2.2. Einphasen- Kerntransformator
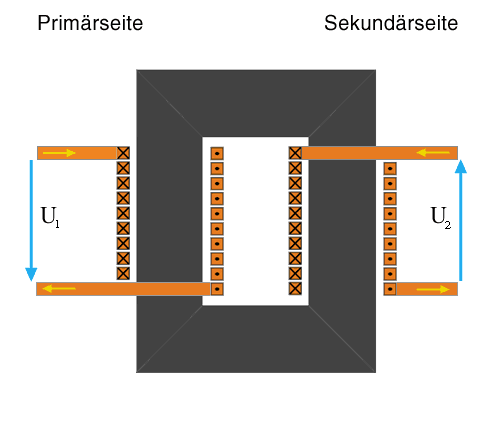
Bild K.4: Kerntransformator mit Primär- und Sekundärwicklung auf verschiedenen Schenkeln
Für größere Leistungen wird oft der Einphasen-Kerntransformator verwendet, weil der Wärmeaustausch der Wicklungen mit der Umgebung dort besser funktioniert. Ein weiterer Grund für die Verwendung des Mantelkerns bei eher kleinen Transformatoren ist die geometrische Unmöglichkeit einen effizienten kreisförmigen Kernquerschnitt aus seinen zwei Blechpaketen herzustellen. Man verschenkt so nämlich bei den Übergängen auf das Joch wertvolle Querschnittsfläche. Bei einem Einphasen- Kerntransformator, der durch Kernschneiden hergestellt wurde, hat man dieses Problem nicht.
2.2.1. Möglichkeiten, die Wicklungen auf dem Kern eines Einphasen- Kerntransformators anzuordnen
Primär- und Sekundärwicklungen über beide Schenkel verteilt:
Bessere Verstellmöglichkeiten des Spannungs / Strombereichs durch Paralell / Reihenschaltung der Wicklungen auf den verschiedenen Schenkeln
Bei dieser Bauweise muß man die Wicklungen im richtigen Sinn zueinander schalten. Wenn man z.B. die primären Wicklungsstränge so verschaltet, daß ihre Magnetfelder sich aufheben, resultiert daraus ein sehr hoher Leerlaufstrom und der Transformator funktioniert nicht.
Primär- und Sekundärwicklungen auf verschiedenen Schenkeln aufgebracht:
Gute Isolation zwischen Primärseite und Sekundärseite durch großen Abstand. Größeres Streufeld, weil jede Seite nur noch die halbe Wickellänge hat.
Die Kernform von gestanzten rechteckigen Kernen dieser Art bezeichnet man mit "UI". Sie wird ähnlich wie die Form "EI" bei Mantelkerntransformatoren abfallos gestanzt und bei kleineren Transformatoren angewendet als das Kernschneideverfahren.
Die Herstellung durch Kernschneiden ermöglicht die Verwendung kornorientierter Bleche. Man hat dann allerdings zwei Luftspalte mehr in dem magnetischen Kreis.
2.3. Ringkerntransformator
Beim Ringkerntransformator sind die Primären und Sekundären Wicklungen über die Länge des ganzen Kerns verteilt. Die mittlere Feldlinienlänge, die für viele Berechnungen benötigt wird, entspricht nicht der Mittellinie in dem Torus, weil innen die Leiter zwangsläufig dichter angeordnet sind als außen. Infolge des Durchflutungssatz ist die mittlere Feldlinienlänge, also die Länge der Trennlinie, die den magnetischen Fluß in zwei gleich große Teile teilt, kürzer als die geometrische Mittellinie.
Das Ferritmaterial eines Ringkerntransformators hat einen geringeren magnetischen Leitwert als Trafobleche, ist aber aufgrund geringerer Wirbelstromverluste besser für hohe Frequenzen geeignet. Es wird verwendet, weil sich Trafobleche ohne Beeinträchtigung ihrer Eigenschaften nicht so stark biegen lassen.
Kernform und Material ermöglichen außerdem die günstige Eigenschaft des Magnetkreises luftspaltfrei zu sein.
Die Leiter müssen bei der Herstellung eines Ringkerntrafos von Hand oder mit einer sehr komplizierten Maschine um den Kern gewickelt werden.
Die Kerne von Drosseln werden auch in den drei hier beschriebenen Bauweisen hergestellt. Größere Drosseln werden dabei häufig als Kern-Typ gefertigt. Kleine Drosseln kann man oft leichter in der Mantelkern- Ausführung bauen. Für Funkentstörung und hohe Frequenzen (z.B. in Schaltnetzteilen) verwendet man Ringkerne aus Ferrit.
Siehe auch:
» Transformator » Wirbelstromverluste » Vorzugsrichtung » Leerlaufverluste » Drehstromtransformator » Magnetische Widerstand Rm » Leerlaufstrom » Drossel » Einschaltstrom » DurchflutungssatzKühlkanal
Der Kühlkanal ist ein radialer Freiraum innerhalb der einzelnen Wicklungen eines Transformators.
Er dient bei einem Trockentransformator dazu, die in den Spulen freiwerdenden Kupferverluste durch Konvektion der Umgebungsluft abzutransportieren (Kühlungsarten). Dabei ist er so ausgelegt, daß die Strömung der Luft turbulent verläuft, damit noch mehr Wärmeaustausch zwischen den Spulen und der Luft stattfindet.
Siehe auch:
» KupferverlusteKühlungsarten
Die bei Transformatoren verwendeten Kühlungsarten werden nach der Art des inneren Kühlsystems und der Art der äußeren Kühlung unterschieden. "Inneres Kühlsystem" bedeutet das Kühlsystem, das mit den Wicklungen in Kontakt tritt.
Die äußere Kühlung dient dazu die Wärme vom Transformator zu entfernen. Sie muß nicht mit Rücksicht auf gute elektrische Isolationseigenschaften konstruiert werden.
Die Kühlungsarten werden nach den Kühlmedien und nach Art des Kühlmittel - Transports unterschieden. Dabei werden die Anfangsbuchstaben der entsprechenden englischen Begriffe verwendet.
Als Kühlmedien für den inneren Kreislauf kommen in Frage:
| Bezeichnung | Kühlmittel |
|---|---|
| "A" | Luft |
| "G" | ein anderes Gas (meist SF6) |
| "K" | Öl |
| "O" | Flüssigkeit mit Brennpunkt über 300°C (z.B. Silikonöl) |
Für den äußeren Kreislauf stehen folgende Kühlmittel zur Auswahl:
| Bezeichnung | Kühlmittel |
|---|---|
| "A" | Luft |
| "W" | Wasser |
Bei normalen Trockentransformatoren, die durch Konvektion der Umgebungsluft funktionieren, gibt es nur ein Kühlsystem.
Weiter unterscheidet man die Art in der das Kühlmedium geführt und transportiert wird:
| Bezeichnung | Kühlmitteltransport |
|---|---|
| "N" | Natürliche Konvektion durch Erwärmung |
| "F" | Forcierte Strömung (durch Gebläse oder Pumpen) Bei forcierter Strömung in einem Ölkreislauf ist die Pumpe so angebracht, daß die gesamte Strömung der Pumpe auch durch den Kühler läuft, weil der Gegendruck des Kühlers die kritische Stelle in dem Kreislauf ist. |
| "D" | Forcierte Strömung, die speziell auf die Wicklungen gerichtet ("directed") ist. Das ist z.B. bei Hochstromtransformatoren mit einem Hohlprofilleiter, durch den Wasser geleitet wird, der Fall. |
Die Bezeichnung der Kühlungsart setzt sich, wenn zwei Kühlsysteme vorhanden sind aus vier Buchstaben zusammen, die wie folgt angeordnet sind:
<Kühlmittel innen> <Kühlmittelbewegung innen> <Kühlmittel außen> <Kühlmittelbewegung außen>
Einige Kühlungsarten als Beispiel:
| Bezeichnung | Bemerkung |
|---|---|
| ONAN | Typischer Öltransformator, der nur mit Konvektion funktioniert. Vorteil: Es können keine Pumpen oder Gebläse ausfallen |
| AN | Trockentransformator wie oben beschrieben |
| ONAF | Öltransformator, der insgesamt etwas kompakter ausfällt, weil die äußeren Ölkühler von Gebläsen belüftet werden und deshalb bei kleinerer Oberfläche die gleiche Verlustleistung abgeben können. |
| OFAF | Wird nur verwendet, wenn die Konvektionskraft des Öls nicht ausreicht. |
| GFAF | Seltener Trafotyp, in dem als inneres Kühlmedium ein Gas mit Überdruck durch die Wicklungen bewegt wird. |
| WDAN | Bei Hochstromtransformatoren mit relativ geringer Spannung kann man Wasser innen durch die Stromleiter leiten. |
| OFWF | Wasserkühlung ist bei sehr hohen Umgebungstemperaturen und wenn die Abwärme z.B. zur Heizung genutzt werden soll sinnvoll. |
Kupferverluste
Die Kupferverluste werden hauptsächlich durch den ohmschen Widerstand der im Transformator verwendeten Leiter hervorgerufen. Der Stromfluß durch diesen Widerstand verursacht eine Verlustleistung, die dann sekundärseitig fehlt.
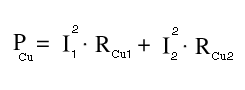
Formel K.1: Berechnung der Kupferverluste aus primären und sekundären Wicklungswiderständen und Stromstärken
Daraus resultiert dort ein geringer Spannungsabfall gegenüber Leerlaufbetrieb.
Bei sehr großen Transformatoren ist neben diesem direkten ohmschen Anteil der K. noch folgende Verlustleistung zu berücksichtigen:
Der Anteil der durch das Streufeld im Kupfer hervorgerufenen Wirbelstromverluste kann nicht mehr vernachlässigt werden. Sie lassen sich in Form einer zusätzlichen, in Reihenschaltung mit der Primärwicklung verketteten Sekundärwicklung darstellen.
Der Widerstand dieser Wicklung sinkt mit steigendem Streufeld, weil die Eindringtiefe der Feldlinien in das Kupfer mit der Flußdichte zunimmt.
Daher steigen diese Verluste im Unterschied zu den normalen Kupferverlusten ungefähr linear mit der Stromstärke an.
Der Kupferwiderstand im Ersatzschaltbild verhält sich deshalb nicht mehr nach dem ohmschen Gesetz und die Ergebnisse, die das Ersatzschaltbild liefert sind für große Transformatoren nicht so exakt.
Dennoch werden diese Wirbelstromverluste den Kupferverlusten zugerechnet. Sie sollten nicht mit den Wirbelstromverlusten des Eisens im Kern oder den größtenteils aus Wirbelstromverlusten bestehenden Zusatzverlusten verwechselt werden.
Bei Transformatoren mit hohen Leiterquerschnitten kann es vorkommen, daß es nicht ausreicht den Gleichstromwiderstand der Wicklungen der Berechnung zugrunde zu legen, sondern man muß die Stromverdrängung berücksichtigen.
Die K. entsprechen bei Nennlast ziemlich genau der Kurzschlußleistung Pk . Sie hängen wie auch der spezifische Widerstand von Kupfer von der Temperatur ab, bei höherer Temperatur werden sie größer.
Siehe auch:
» Kurzschlußspannung » Streufeld » Wirbelstromverluste » Eisenverluste » Kern » Zusatzverluste » Stromverdrängung » KurzschlußverlusteKurzschlußfestigkeit
Die Kurzschlußfestigkeit teilt sich in zwei Teile auf:
1. Mechanische Kurzschlußfestigkeit
Diese Kurzschlußfestigkeit ist die ausreichende mechanische Belastbarkeit eines Transformators und der Zuleitungen für die an anderer Stelle beschriebenen Lorentzkräfte. Die Kräfte müssen für den Spitzenwert des Kurzschlußstroms Ik berechnet werden.
Diese Art Kurzschlußfestigkeit ist eine Grundvoraussetzung für jeden Transformator.
Zusätzlich muß er noch in gewissem Umfang eine zweite Art von K. erfüllen:
2. Thermische Kurzschlußfestigkeit
Im Kurzschlußfall werden große Transformatoren mit einer Wärmeentwicklung konfrontiert, die weit über dem liegt, was im zulässigen Temperaturbereich abgegeben werden kann.
Die Wärmekapazität der verwendeten Materialien speichert jedoch die Wärme und sorgt für einen vorteilhaften gleichmäßigen Anstieg der Temperatur.
Der Transformator muß in jedem Fall so konstruiert sein, daß er diesem Temperaturanstieg standhält, bis die Schutzeinrichtungen ansprechen. (Thermisches Modell eines Transformators)
Nach Norm gilt für die meisten Transformatoren eine Kurzschlußdauer von 2 Sekunden.
Siehe auch:
» Transformator » Lorentzkraft » KurzschlußstromKurzschlußspannung
Die Kurzschlußspannung uk ist neben dem Leerlaufstrom eine wichtige Kenngröße des Transformators. Die K. bezeichnet die Spannung, die man an der Primärseite eines Transformators anlegen muss, damit bei kurzgeschlossener Sekundärseite der Bemessungsstrom des Transformators fließt.
Dieser Wert wird meist in Prozent von der primären Bemessungsspannung angegeben. Üblich sind 3,5 bis 5 Prozent.
Die in diesem Betriebszustand umgesetzte Wirkleistung bezeichnet man als Kurzschlußverlustleistung Pk. Sie entspricht ungefähr der Kupferverlustleistung, weil sie hauptsächlich an dem Kupferwiderstand der Wicklungen umgesetzt wird.
Die Kurzschlußspannung wird außer durch diesen Wirkwiderstand auch durch die Streuinduktivität verursacht, die jedoch nur Blindleistung umsetzt. ( Ersatzschaltbild)
Daher ist die Zerlegung der K. uk in einen Wirkanteil uR und einen Blindanteil j uσ üblich.
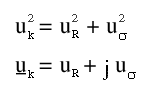
Formel K.2: Zusammensetzung der Kurzschlußspannung als reelle und komplexe Größe
Man kann die K. auch als Spannungsabfall der Ausgangsspannung bei Nennlast gegenüber dem Wert im Leerlaufbetrieb betrachten, wobei sie rechnerisch auf die Sekundärseite transformiert werden muß und dann mittels Vektoraddition abgezogen wird.
Bei der Paralellschaltung von Transformatoren ist die K. eine wichtige Größe, weil sie Aufschluß über die Impedanz des Transformators gibt. Von diesem Wert ist die Verteilung der Belastung paralell geschalteter Transformatoren stark abhängig.
Man muß deshalb häufig die nötige K. vor der Konstruktion des Transformators spezifizieren, um sie dann durch die richtige Größe des Streufelds durch passende Anordnung der Wicklungen zu erreichen.
Siehe auch:
» Wirkleistung » Kurzschlußverluste » Kupferverluste » StreufeldKurzschlußstrom
Den Kurzschlußstrom eines Transformators kann man sehr einfach berechnen, indem man den Kehrwert des des Betrags der Kurzschlußspannung in Prozent bildet und das Ergebnis mit dem hundertfachen primären Bemessungsstrom multipliziert.
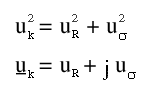
Formel K.3: Berechnung des Kurzschlußstroms aus der Kurzschlußspannung in Prozent
Das Ergebnis ist jedoch nur ein Näherungswert, weil in dieser Formel der komplexe Widerstand des Stromnetzes auf der Primärseite nicht berücksichtigt wird. Es wird einfach angenommen, daß das Stromnetz keinen Innenwiderstand hat.
Dieser Widerstand müßte zu dem Innenwiderstand des Transformators addiert werden, den man aus Kurzschlußspannung erhält. Wenn man einen relativ kleinen Transformator an ein Netz mit relativ hoher Kurzschlußleistung anschließt, kann man den Netzwiderstand leicht vernachlässigen.
Für einige Berechnungen, die mit dem K. durchgeführt werden, ist es notwendig den Spitzenwert auszurechnen, den man durch Multiplikation mit ![]() erhält.
erhält.
Wenn bei einer Kurzschlußmessung der Zeitraum der Messung keine ganzahlige Anzahl an Halbwellen umfaßt, muß die Phasenlage am Anfang und Ende der Messung mit berücksichtigt werden. Die entstandene Wärmemenge steigt aufgrund der Sinusform des Kurzschlußstroms nämlich nicht gleichmäßig mit der Zeit an.
Bei einer 2 s - Messung hat man immer 200 Halbwellen und braucht sich deshalb um die Phasenlage keine Gedanken zu machen.
Siehe auch:
» KurzschlußspannungKurzschlußverluste
Die Kurzschlußverluste geben an, wieviel Wirkleistung umgesetzt wird, wenn ein Transformator bei kurzgeschlossener Sekundärwicklung primär mit Bemessungsstrom durchflossen wird. Die dann anliegende Spannung nennt sich Kurzschlußspannung. Das Formelzeichen für die Kurzschlußverluste ist Pk.
Diese Leistung entspricht, wenn man die Zusatzverluste, die auch ein Bestandteil der Kurzschlußverluste sind, außer acht läßt, der Kupferverlustleistung im Betrieb bei Abgabe der Bemessungsleistung. Die Kupferverlustleistung wiederum besteht größtenteils aus der vom Bemessungsstrom an dem ohmschen Widerstand der Leiter umgesetzten Leistung.
Zusammenfassend kann man sagen, daß alle Verluste, die irgendwie von der Stromstärke, also der Belastung des Transformators, abhängen zu den Kurzschlußverlusten gezählt werden.
Der Anteil der Eisenverluste an den Kurzschlußverlusten ist meistens vernachlässigbar gering.
Siehe auch:
» Wirkleistung » Bemessungsstrom » Kurzschlußspannung » Zusatzverluste » Kupferverluste » Bemessungsleistung » EisenverlusteLeerlaufstrom
Der L. bezeichnet den Strom, der bei anliegender Bemessungsspannung in die Primärseite eines Transformators fließt, während die Sekundärseite unbelastet ist. Er hat das Formelzeichen I0.
Der hier betrachtete L. bezieht sich auf den eingeschwungenen Zustand. Im Unterschied dazu bezeichnet der Einschaltstrom den Übergang vom unmagnetisierten Transformator zum Leerlaufstrom.
Der Leerlaufstrom hat einen Wirk- und einen Blindanteil. Der Wirkanteil, der Strom der Leerlaufverlustleistung, wird durch die Eisenverluste verursacht, die sich in Hystereseverluste und Wirbelstromverluste aufteilen.
Der Blindanteil ensteht durch die endliche Hauptinduktivität eines realen Transformators (der magnetische Widerstand des Kerns ist nicht 0). Je kleiner eine Induktivität ist, die man an das Netz anschließt, desto größer wird der Blindstrom der fließt. Um die Verluste in den Zuleitungen gering zu halten, versucht man den Leerlaufstrom zu minimieren.
Außerdem kann ein zu hoher Leerlaufstrom das Netz stören, weil reale Netze durch Verbraucher beeinflußt werden können (kein unendlich kleiner Innenwiderstand der Spannungsquelle, Leitungswiderstand nicht 0).
Die Hysteresekurve ist nämlich nicht linear und führt, wenn man sie mit der Sinuswelle der integrierten Eingangspannung verkettet zu einer stark oberwellenhaltigen Stromentnahme, d.h. der Leerlaufstrom ist nicht nur auf die Netzfrequenz beschränkt, sondern enthält Spektralanteile bei den ganzzahligen Vielfachen dieser Frequenz.
Diese zusätzlichen Frequenzanteile können elektronische Verbraucher stören, die oft nur durch das Ausfiltern der 50 Hz - Frequenz vor Beeinflussung geschützt sind. Wegen der Dimensionierung der Netze für eine Stromentnahme, die deutlich über dem L. liegt, kann man die Oberwellen jedoch meistens vernachlässigen.
Die Auswirkungen des Frequenzspektrums des L. auf einen Drehstromtransformator hängen mit von seiner Schaltgruppe ab.
Durch Betrachtung der Sinusfunktionen der Eingangströme kommt man darauf, daß die Ströme der Oberwellen mit einem durch drei teilbaren Vielfachen der Netzfrequenz sich wie eine gleichphasige Belastung verhalten, weil sich die drei Phasen durch Multiplikation des Winkelarguments mit drei immer in der selben Phasenlage befinden (120° x 3 = 360°).
Bei der primärseitigen Schaltgruppe Y führt ein solches Verhalten zu einem unerwünschten Streufeld, bei Schaltgruppe D können die gleichphasigen Anteile des Stroms frei fließen. Vielfache der Netzfrequenz, die nicht durch drei teilbar sind, sind entweder gegenphasig oder verlaufen in der selben Drehrichtung, wie die Eingangspannung, bloß schneller. Diese beiden Fälle sind unproblematisch.
In der Realität kann der L. bei baugleichen Transformatoren um bis zu 30% schwanken, weil schon ein sehr kleiner Luftspalt im Kern den magnetischen Widerstand deutlich erhöht. Geringe Fertigungstoleranzen führen also zu einem großen Unterschied im Leerlaufstrom. Solange der L. im zulässigen Rahmen bleibt resultieren daraus keine negativen Folgen, auch das Übersetzungsverhältnis ändert sich kaum.
Siehe auch:
» Bemessungsspannung » Einschaltstrom » Eisenverluste » Hystereseverluste » Wirbelstromverluste » Induktivität » Magnetische Widerstand Rm » Hysteresekurve » Drehstromtransformator » Kern » ÜbersetzungsverhältnisLeerlaufverluste
Die L. sind die Messgröße, die man erhält, indem man am sekundärseitig unbelasteten Transformator primär die Bemessungsspannung anlegt und dann die aufgenommene Wirkleistung bestimmt. Das Formelzeichen ist P0.
Die L. bestehen größtenteils aus den Eisenverlusten, so daß man beide gleichsetzen kann.
Der dabei vernachlässigte Anteil sind ohmsche Verluste in den Wicklungen aufgrund des Leerlaufstroms und die Wirbelstromverluste der Wicklungen, die ebenso wie Zusatzverluste am Gehäuse des Transformators, durch das Streufeld des magnetischen Hauptflusses hervorgerufen werden können. Der oberwellenhaltige Leerlaufstrom verursacht über den Streufluß der primären Streuinduktivtät auch Wirbelstromverluste im Kupfer und Zusatzverluste.
Die im vorigen Absatz aufgezählten Wirbelstromverluste und Zusatzverluste müssen jedoch von denen, die den Kurzschlußverlusten zugerechnet werden, unterschieden werden.
Im allgemeinen sind sie so gering, daß sie überhaupt nicht berücksichtigt werden müssen. Nur bei außergewöhnlich streufeldbehafteten Kernformen und großen Leiterquerschnitten spielen sie eine Rolle.
Siehe auch:
» Bemessungsspannung » Wirkleistung » Leerlaufstrom » Wirbelstromverluste » Streufeld » KurzschlußverlusteLenzsche Regel
Die Lenzsche Regel besagt, daß die induzierte Spannung immer die Polarität hat, in der der von ihr verursachte Strom durch sein Magnetfeld der Ursache der Induktion, der Magnetfeldänderung, entgegenwirkt.
Die L. stellt also dar, wie die Physik versucht, den Ist - Zustand aufrecht zu erhalten. Sie ist letztlich eine Sonderform des Energieerhaltungssatz.
Wichtig bei der Anwendung der L. ist die Richtung der Ursache der Induktion richtig festzustellen. Die Ursache einer Induktion ist nämlich immer die Änderung eines Magnetfelds ( Induktionsgesetz). D.h. wenn die Magnetfeldstärke abnimmt, zeigt die Richtung der Ursache genau in entgegengesetzte Richtung zu den Feldlinien. Der induzierte Strom versucht dann das Magnetfeld aufrecht zu erhalten.
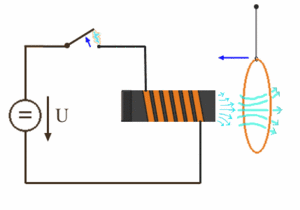
Bild L.1: Anziehung einer frei aufgehängten Leiterschleife beim Abschalten des felderzeugenden Stroms
Die obige Abbildung zeigt, daß die Feldlinien, die in der Leiterschleife durch den induzierten Strom verursacht werden und die Feldlinien, die die felderzeugende Spule während des Abschaltens noch für einen kurzen Augenblick hervorbringt, die gleiche Richtung haben.
Dieses Verhalten führt zu einer Anziehung der Leiterschleife und beruht auf der Stromrichtung des induzierten Stroms, die nach der Lenzschen Regel bestimmt werden kann.
Dabei spielt die Polarität der anliegenden Spannung und der Wickelsinn der Spule keine Rolle; die Leiterschleife wird beim Abschalten immer angezogen.
Die Rechte-Hand-Regel ergänzt die Lenzsche Regel so, daß die Richtungen, die in der L. in Relation zueinander gesehen werden, absolut bestimmt werden können.
Siehe auch:
» Induktion » Induktionsgesetz » FeldlinienLorentzkraft
Die Lorentzkraft ist die Kraft, die von Magnetfeldern auf bewegte elektrische Ladungen ausgeübt wird.
Es ist die folgende grundlegende Beschreibung der Lorentzkraft, die, wo es möglich ist, Begriffe aus der Mechanik (Kraft, Geschwindigkeit) verwendet, üblich:
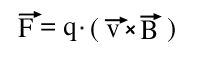
Formel L.1: Kraft F auf Ladung q, die sich mit Geschwindigkeit v durch ein Magnetfeld B bewegt.
Die Lorentzkraft beruht auf der Wechselwirkung des Magnetfelds bewegter Elektronen mit dem Magnetfeld der Umgebung. So ensteht eine Kraft, die freie Elektronen, die sich in einem Magnetfeld senkrecht zu den Feldlinien bewegen, auf eine Kreisbahn zwingt.
Die Richtung der Kraft, die über das Kreuzprodukt in der Formel (das "x") vorgegeben ist, kann auch durch die Rechte-Hand-Regel bestimmt werden.
Wenn man sich eine bewegte Ladung im Magnetfeld vorstellt und um die Ladung herum einen schmalen, unendlich langen Streifen senkrecht zur Bewegungsrichtung herausschneidet, stellt man fest, daß die Änderung des magnetischen Flusses durch die Bewegung der Ladung auf einer Seite größer ist als auf der anderen. Die bewegte Ladung ist nämlich von einem sich vergrößernden und einem immer kleiner werdenden Rechteck auf jeder Seite umgeben. Entlang der Seiten dieser Rechtecke, die sich aus den gerade beschriebenen Streifen zusammensetzen, wird eine Spannung induziert, die die Ladung gemäß der Lorentzkraft ablenkt. Die Lorentzkraft ist also nur eine spezielle Formulierung des Induktionsgesetzes.
Man kann bewegte Ladungen auch als Ströme auffassen. Daher wirkt die L. auch auf die Elektronen eines kontinuierlichen Stromflusses. Dabei ist zu beachten, daß Elektronen eine negative Ladung haben und die technische Stromrichtung der Elektronenbewegungsrichtung entgegengesetzt ist. Also zeigt die technische Stromrichtung letztendlich in Richtung des mit der Ladung q multiplizierten v - Vektors der Formel.
Die Auswirkung der Lorentzkraft auf gegensinnige Stromflüsse, die z.B. innerhalb eines Stromkreises vorkommen, und sich zwangsläufig gegenseitig mit Magnetfeldern durchfluten, ist in der folgenden Darstellung beschrieben:
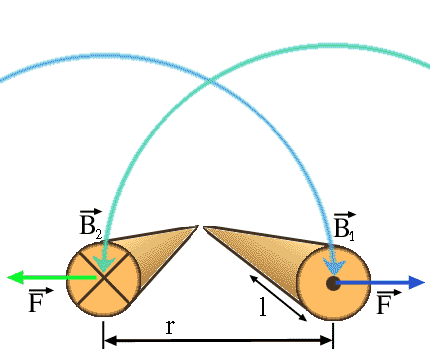
Bild L.2: Lorentzkraft, die zwei Ströme innerhalb eines Streckenabschnitts l auseinanderdrückt.
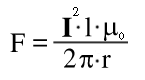
Formel L.2: Kraft auf Abschnitt l zwischen zwei gegensinnigen Strömen I im Abstand r
Die Flußdichte, die dazu dient die Lorentzkraft in diesem Fall zu berechnen, basiert auf dem Durchflutungsatz. In dem Bild wirkt sie in Form einer Streckenlast. Um die Kraft zu bestimmen muß man sich also auf einen Leiterabschnitt einer bestimmten Länge beziehen.
Elektronen in metallischen Leitern können sich zwar innerhalb des Leiters frei bewegen, werden aber daran gehindert den Leiter zu verlassen. Daraus folgt, daß sich eine L. auf den Leiter und das damit verbundene mechanische System überträgt.
Daher ist die L. in elektrischen Maschinen nutzbar. Der durch das magnetische Drehfeld der Ständerwicklung induzierte Strom in einem Kurzschlußläufer ist z.B. immer so gerichtet, daß sie ein gleichmäßiges Drehmoment auf den Läufer ausübt.
Die L. kann, wenn sie unbeabsichtigt auftritt, auch schädliche Auswirkungen haben. In Transformatoren kann sie zu einer mechanischen Zerstörung führen, wenn sie durch einen Blitzeinschlag oder Kurzschluß so schnell ansteigt, daß Schutzeinrichtungen nicht früh genug ansprechen können.
Die Kräfte, die so enstehen, können, falls der Transformator nicht entsprechend ausgelegt ist, bei einem sekundären Kurzschluß einen axialen Schaden verursachen, weil sich die Wicklungen gegenseitig abstoßen und dabei gegen das Joch des Transformators prallen.
Wenn man einen Transformator kurzschlußfest konstruieren will, muß man diese Kräfte durch entsprechende Abstützungen und Verstärkungen auffangen. Ihre Ursache liegt in einem geringfügigen Versatz der Wicklungen gegeneinander aufgrund von Abweichungen in der Wicklungslänge.
Die hier beschriebene Art der Beschädigung ist bei Überspannung nicht so häufig wie die andere Möglichkeit:
Bei einem Kurzschluß oder einer primären Überspannung (z.B. in Folge eines Blitzeinschlags) kann es dazu kommen, daß sich die Wicklungen radial auseinander ziehen. Bei Transformatoren mit eckigen Wicklungen kann das einen Durchbruch der Isolation an den Stellen, wo sie mit dem Kern zusammenstößt, zur folge haben. Durch den hohen Stromfluß können sich sogar die Zuleitungen verbiegen.
Die radiale Ausdehnung der Primärwicklung beruht darauf, daß bei kreisförmigen Strömen die gegenüberliegende Seite eines Punktes auf dem Kreis immer einen Stromfluß in die entgegengesetzte Richtung trägt. Gegenüberliegende Punkte stoßen sich also ab; die Wicklung hat das Bestreben ihren Radius zu vergrößern.
Bei größeren Transformatoren, wo die Primärwicklung immer außen angeordnet ist, wirken diese Zugkräfte nur auf die Primärwicklung; die innenliegende Sekundärwicklung wird zusammengedrückt.
Eine sinnvolle Gegenmaßnahme ist in jedem Fall die Verwendung runder Wicklungen und Kerne, so daß die auftretenden Kräfte keine Biegemomente sondern nur Zug- und Druckkräfte in den Leitern zur Folge haben. Das ist auch ein wichtiger Grund, warum Transformatoren ab einer gewissen Größe zylinderförmige Wicklungen haben.
Die Lorentzkraft hoher Ströme ist deshalb so problematisch, weil sie im Quadrat zur Stromstärke ansteigt.
Siehe auch:
» Feldlinien » Induktionsgesetz » Durchflutungssatz » KurzschlußfestigkeitMagnetische Durchflutung Θ
Die magnetische Durchflutung wird auch als magnetische Spannung V bezeichnet.
Definition der magnetischen Durchflutung für Abschnitte mit konstanter magnetischer Erregung: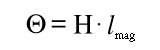
Formel M.1: Abschnittsdurchflutung für Bereiche mit konstanter Feldstärke
Die Einheit der magnetischen Durchflutung ist ein Ampere [A].
Man kann sich die D. als magnetfelderzeugende zentrale "Kraft" vorstellen.
Definition der Durchflutung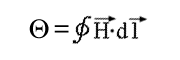
Formel M.2: Definition der Durchflutung
Genau wie sie der Spannung im elektrischen Stromkreis gegenübersteht, gibt es analog zur elektrischen Feldstärke E [V/m] die magnetische Feldstärke (oder auch magnetische Erregung) H [A/m] im Magnetkreis.
Abschnittsweise Durchflutungen in Bereichen mit unterschiedlichem magnetischen Widerstand verhalten sich zur Gesamtdurchflutung wie elektrische Spannungen an einem Spannungsteiler zur Gesamtspannung. (Durchflutungssatz)
Aus dem Durchflutungssatz wird klar, daß die Durchflutung bei Spulen mit mehreren Windungen stufenweise mit der Windungszahl steigt.
Der selbe Strom wird dabei immer wieder aufsummiert.
Siehe auch:
» Magnetische Erregung H » Magnetische Widerstand Rm » DurchflutungssatzMagnetische Erregung H
Die magnetische Erregung H ist ein Maß für die Verursachung einer magnetischen Flußdichte.
Andere Bezeichnungen für diese Größe sind magnetische Feldstärke und Magnetisierung, falls es um die durch den Polarisierungszustand eines Materials verursachte Feldstärke geht.
Sie wird in A/m gemessen und ist daher sowohl von dem fließenden Strom als auch von der geometrischen Anordnung des elektrischen Leiters, sowie der Verteilung der magnetischen Werkstoffe abhängig.
Die E. steigt durch die Summierung der Wirkungen bei gleichem Strom linear mit der Windungszahl. Das folgt aus dem Durchflutungssatz, der dazu dient die Verteilung der magnetischen Erregung anhand des fließenden Stroms zu bestimmen. Sie ist genau wie die Induktion eine ortsabhängige, gerichtete Größe. Der Zusammenhang zwischen E. und Induktion wird durch die Formel
Formel: magnetische Erregung H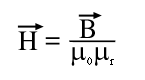
Formel M.3: Magnetische Erregung in Abhängigkeit von der Permeabilität
wiedergegeben.
Daher vergrößert sich in einem Luftspalt des magnetischen Kreises die magnetische Erregung und damit auch die Energie pro Volumen des Magnetfelds ( Hystereseverluste ). Weil das System den Zustand niedrigster Energie annehmen möchte, bildet sich eine Kraft, die den Luftspalt schließen will. Diese Kraft berechnet man auf folgende Weise:
Formel für die Haltekraft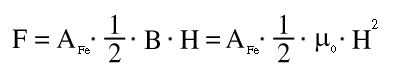
Formel M.4: Kraft die durch ein Feld mit einer magnetischen Erregung H in Luft hervorgerufen wird
Nach Induktionsgesetz und Spannungserzeugungsformel bleibt bei konstanter Spannung an einer Spule der Fluss Φ im Luftspalt nämlich immer gleich und die Stromstärke ändert sich je nach Länge des Luftspalts.
Siehe auch:
» Magnetische Flußdichte » Durchflutungssatz » Induktion » Permeabilität » Hystereseverluste » Induktionsgesetz » SpannungserzeugungsformelMagnetische Flußdichte
Als magnetische Flußdichte, magnetische Induktion, magnetische Kraftflußdichte, oder in dem entsprechenden Kontext magnetische Polarisation J bezeichnet man die Dichte der Wirkung des Magnetfelds pro Flächeneinheit. In Formeln wird hierfür ein B verwendet.
Den Betrag dieser Größe kann man sich als abhängig von der Anzahl der Feldlinien pro Flächeneinheit vorstellen.
magnetische Flußdichte![]()
Formel M.6: Magnetische Flußdichte in Abhängigkeit von magnetischer Erregung und Permeabilität
Die F. gibt aufgrund ihrer Vektornatur Aufschluß über die Stärke und Richtung der magnetischen Einwirkung auf einen bestimmten Ort. Sie wird in der Einheit Vs/m2 gemessen, die mit Tesla (T) bezeichnet wird. Früher war die Einheit ein Gauss, was 0,0001 Vs/m2 entspricht. Wenn man die F. über eine die Eisenquerschnittsfläche eines Transformators integriert bekommt man den wirkenden magnetischen Fluß als Ergebnis.
Siehe auch:
» Feldlinien » Magnetischer Fluß ΦMagnetische Verkettung Ψ
Die magnetische Verkettung Ψ hat die selbe Einheit wie der Fluß. Sie läßt sich anstelle des Flusses in das Induktionsgesetz einsetzen.
Die V. beschreibt einen Fluß, der auf mehrere Windungen einwirkt, die den Fluß in bezug auf die Induktionswirkung verketten, weil sie in Reihe geschaltet sind. Diese Verkettung wird in die Größe mit einbezogen.![]()
Formel M.7: Definition der Magnetischen Flußverkettung
Man kann auch darauf verzichten die Verkettung mit einem eigenen Formelzeichen zu definieren und stattdessen direkt N * Φ in die entsprechenden Formeln einsetzen.
Obwohl die vom Fluß durchsetzte Fläche nicht kreisförmig sondern schraubenförmig ist, kann mit dem Faktor N gerechnet werden, sofern der betrachtete Fluß senkrecht durch die Spule tritt (was nicht der Fall ist, wenn das Feld von der Spule selbst erzeugt wird.
Induktivität).
Die Senkrechten der Fläche stehen zwar immer etwas schräg zur Längsrichtung, aber die Fläche ist auch insgesamt größer als entsprechende Kreisflächen, so daß das Ergebnis das selbe ist.
Siehe auch:
» Magnetischer Fluß Φ » Induktionsgesetz » InduktivitätMagnetische Widerstand Rm
Der magnetische Widerstand Rm entspricht dem mit N2 multiplizierten Kehrwert der Induktivität, die durch N2 geteilt gleich dem magnetischen Leitwert ist. N bezeichnet dabei die Anzahl der auf den betrachteten Kern aufgebrachten Windungen.
Der magnetische Widerstand bezieht sich also nicht auf die Windungszahl, sondern beschreibt nur den Kern einer elektrischen Maschine.
Formel: magnetischer Widerstand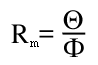
Formel M.8: Definition des magnetischen Widerstands Rm
Die Einheit von Rm ist daher A/Vs. Der Wert gibt an, wieviel magnetische Durchflutung man braucht, um einen bestimmten Fluß zu erzeugen.
Der W. eines Kerns kann aus seiner magnetischen Länge lm und der Permeabilität des Kernmaterials errechnet werden. Bei der Verwendung unterschiedlicher Materialien können die magnetischen Widerstände, bzw. bei Paralellschaltung, die Leitwerte der einzelnen Stränge addiert werden, vorausgesetzt sie verhalten sich linear wie ohmsche Widerstände. Ziel bei der Konstruktion eines Transformators ist es, einen möglichst geringen magnetischen Widerstand des Kerns zu erreichen.
Siehe auch:
» Induktivität » Magnetische Durchflutung Θ » Magnetischer Fluß Φ » Permeabilität » KernMagnetischer Fluß Φ
Der Fluß Φ ist ein Maß, das den Umfang eines Magnetfelds für eine bestimmte Querschnittsfläche wiedergibt. Der Fluß wird in der Einheit Weber (Wb) gemessen, die einem Vs entspricht. Die Ursache für den Fluß ist eine magnetische Durchflutung Θ, die durch den fließenden Strom verursacht wird. Außerdem ist er abhängig von der Permeabilität des Materials, das er durchquert.
Der Fluß durch eine Fläche wird immer durch Integrieren der Flußdichte in Richtung der Oberflächenormalen dA der Fläche errechnet.
D.h. der Fluß einer Fläche bezieht automatisch nur senkrechte Anteile des Magnetfelds mit ein. Das ist bei allen Formeln zu beachten, in denen er vorkommt. Durch folgende Formel werden diese Verhältnisse wiedergegeben:
Definition des magnetischen Flusses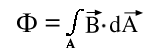
Formel M.5: Definition des magnetischen Flusses
Daher bezieht man sich, wenn man von einem magnetischen Fluß redet, oft unbewußt auf eine dazugehörige Fläche.
Bemerkenswert ist, daß der Fluß durch abgeschlossene Oberflächen von Körpern wie Würfel oder Kugeln immer 0 ist. ( Feldlinien )
Für Bereiche mit konstanter Flußdichte in Richtung der Oberflächennormalen ergibt sich Φ = B *A
Das Induktionsgesetz erklärt den Zusammenhang zwischen zeitlicher Änderung des Flusses und induzierter Spannung.
( Spannungserzeugungsformel )
Siehe auch:
» Magnetische Durchflutung Θ » Permeabilität » Feldlinien » Induktionsgesetz » SpannungserzeugungsformelPermeabilität
Die Permeabilität ist ein Maß dafür, wie gut in einem Stoff die magnetische Erregung H in eine Flußdichte B umgesetzt wird. Die Permeabilität ist ein materialspezifischer Wert, der bei ferromagnetischen Stoffen sowohl von der Temperatur und der Richtung der Feldlinien ( Vorzugsrichtung ) als auch von der Größe der Flußdichte ( Hysteresekurve ) und der Frequenz des Magnetfelds abhängen kann. Bei den meisten anderen Stoffen kann man sie als Konstante ansehen.
Sie wird meistens mittels einer relativen Permeabilität angegeben, die sich auf die absolute Permeabilität des Vakuums - die Naturkonstante
µ0 =![]() π 10-6 - bezieht.
π 10-6 - bezieht.
Diese relative Permeabilität ist als einfacher Multiplikationsfaktor eine dimensionslose Größe.
µ0, die Größe, die vervielfacht wird, hat die Einheit eines spezifischen magnetischen Leitwerts. Sie ist eine Naturkonstante, die aus der Definition eines Amperes über die Kraft zwischen zwei Leitern ( Lorentzkraft ) errechnet werden kann. Daher war die willkürliche Festlegung dieser Naturkonstante auf ![]() π 10-6 im SI-Einheitensystem entsprechend der Festlegung des Amperes möglich.
π 10-6 im SI-Einheitensystem entsprechend der Festlegung des Amperes möglich.
Die eigentliche Permeabilität µ in einem magnetischen Werkstoff erhält man aus folgender Formel:![]()
Formel P.1: Die Permeabilität als Produkt von relativer Permeabilität und der Permeabilität des Vakuums
Wobei zwischen Flußdichte und magnetischer Erregung in einem idealen, nicht ferromagnetischen, Material immer folgender Zusammenhang besteht:![]()
Formel P.2: Die Flußdichte ist von der Permeabilität abhängig
Die relative Permeabilität µr ist eine Konstante, die in vielen Fällen den anderen Bedingungen entsprechend einer Tabelle entnommen werden kann.
Für Wechselstrom-Magnetisierung eines ferromagnetischen Stoffs muß man angeben, welche Feldstärke man auf welche Polarisation bezieht, weil der Wert der Permeabilität beim Durchlauf der Hysteresekurve ständig schwankt.
Die P. ist also eine Funktion der Feldstärke:![]()
Formel P.3: Wie Formel P.2 bloß mit variabler Permeabilität für ferromagnetische Werkstoffe
Man kann, wenn man in solchen Fällen mit einer einzigen Permeabilitätszahl rechnen will, den Effektivwert der magnetischen Erregung auf den Effektivwert der Flußdichte beziehen.
Wenn man nur mit den Spitzenwerten der Hysteresekurve rechnet bezeichnet man den Wert als Amplituden-Permeabilität µa. Um die Induktivität des Gesamtsystems für einen Stromkreis zu bestimmen, muß man sich auf die Effektivwerte beziehen. Dann kann man mit den resultierenden Blindleistungen und -strömen ein elektrisches System im stationären Zustand berechnen.
Häufig beziehen sich nämlich die bei der Konstruktion von elektischen Maschinen angegebenen Flußdichten implizit auf Spitzenwerte (eigentlich müsste man dann das Formelzeichen ![]() verwenden)
verwenden)
Siehe auch:
» Magnetische Erregung H » Flussdichte B » Vorzugsrichtung » Hysteresekurve » Lorentzkraft » Magnetische Flußdichte » BlindleistungPrimär- und Sekundärseite
Die Primär- und Sekundärseite eines Transformators ist nach VDE 0532 durch die normale Richtung des Energieflusses vorgegeben.
Die Seite, die Energie aufnimmt, ist die Primärseite; die andere Seite, die Energie abgibt wird als Sekundärseite bezeichnet. Natürlich kommt es im Leerlaufbetrieb auch vor, daß die Sekundärseite keine Energie abgibt.
Diese Bezeichnungen sind unabhängig von den jeweiligen Bemessungsspannungen.
Ein Transformator kann auch mehrere Sekundärwicklungen haben, die dann aber entsprechend der oben stehenden Definition nicht Bezeichnungen wie z.B. "Tertiärwicklung" erhalten.
Weil die Spannung von wenigen großen Transformatoren an Kraftwerken hochgespannt wird und dann schrittweise von immer mehr immer kleineren Transformatoren heruntertransformiert wird, fällt bei der großen Mehrheit der Transformatoren die Primärseite mit der Oberspannungsseite zusammen.
Deshalb wird, wenn man von Oberspannungs- ("OS") Seite redet oft vorausgesetzt, daß es sich dabei um die Primärseite handelt.
Die Unterspannungs- ("US") Seite wird also als Sekundärseite angesehen.
Das Verhalten eines Transformators ist, wenn die Richtung des Energieflusses umgekehrt wird (und dabei natürlich die Bemessungsspannungen der Wicklungen beachtet werden), nicht völlig symmetrisch zu der normalen Betriebsrichtung. Das ist aus dem Ersatzschaltbild ersichtlich, wenn für die Bestimmung der elektrischen Größen im Leerlauf, der Längszweig der jeweiligen Sekundärseite weggelassen wird.
Zum Beispiel kann sich auch das Verhältnis von Einschaltstrom zu Bemessungsstrom deutlich verändern, weil die Streuinduktivtäten auf beiden Seiten unterschiedlich sind.
Daher macht es Sinn Primär- und Sekundärseite fest vorzugeben, auch wenn der Eingangs- und Ausgangsspannung wie z.B. bei einem Trenntransformator genau übereinstimmen.
Siehe auch:
» Bemessungsspannung » EinschaltstromScheinleistung
Die S. wird mit dem Buchstaben S bezeichnet und in VA gemessen. In vektorieller Darstellung bilden Blindleistung, Wirkleistung und Scheinleistung als skalare Größen entlang der hier dargestellten Zählpfeile immer ein rechtwinkliges Dreieck.
S-P-Q Dreieck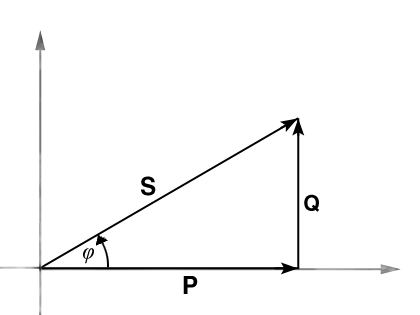
Bild B.1: Das S-P-Q Dreieck
Deshalb kann man mit dem Satz des Pythagoras aus zwei dieser Größen die Dritte errechnen.
Die S. ist in dem Dreieck die geometrische Addition von Wirkleistung und Blindleistung:
Geometrische Addition von Wirkleistung und Blindleistung![]()
Formel S.2: Geometrische Addition von Wirkleistung und Blindleistung
In der komplexen Ebene gilt folgende Formel:
Die Scheinleistung als Produkt der Beträge von Spannung und Strom![]()
Formel S.3: Die Scheinleistung als Produkt der Beträge von komplexer Spannung und komplexem Strom
Wobei die Beträge von komplexer Spannung und Strom, von denen das Produkt gebildet wird, jeweils mit den Abständen der entsprechenden Punkte auf der komplexen Ebene vom Nullpunkt in der Mitte übereinstimmen.
Aus der Formel läßt sich also die Formel S.2 herleiten.
Die Scheinleistung ist die Grundlage für die Dimensionierung des Transformators, der ein Stromnetz versorgt. Das ist der Grund, warum die Leistung eines Transformators in kVA und nicht in kW angegeben wird.
Siehe auch:
» Blindleistung » WirkleistungSpannungserzeugungsformel
Die Spannungserzeugungsformel dient dazu, die primäre Windungszahl eines Transformators aus dem Kernquerschnitt, der Flußdichte und der primären Bemessungsspannung zu berechnen.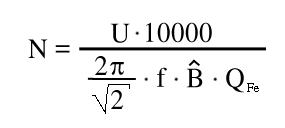
Formel S.3: Die Spannungserzeugungsformel (f in Hertz, B in Tesla und Qfe in cm2)
Das Ergebnis der Formel wird auf die nächste ganze Zahl aufgerundet.
Die sekundäre Windungszahl berechnet sich dann aus dem Verhältnis der Bemessungsspannungen.
Selbstverständlich läßt sich auch jede andere Größe in der Spannungserzeugungsformel aus den restlichen bestimmen.
Meistens wird aber der Kernquerschnitt nach der Bemessungsleistung des Transformators ausgewählt, wobei die Bemessungspannung, Frequenz und Flußdichte auch schon vorgegeben sind, während die primäre Windungszahl gesucht wird.
Grundlage für die Spannungserzeugungsformel ist das Induktionsgesetz wenn es unter Berücksichtigung der magnetischen Flußverkettung formuliert wird. Dabei wird der Effektivwert der Ableitung ![]() gebildet, indem der Spitzenwert des magnetischen Flusses mit 2 π f / 2½ multipliziert wird. 2 π f ist die Ableitung der Sinusfunktion des Flußdichteverlaufs und 2-½ ist der Umrechnungsfaktor vom Spitzenwert der Flußdichte in den Effektivwert.
gebildet, indem der Spitzenwert des magnetischen Flusses mit 2 π f / 2½ multipliziert wird. 2 π f ist die Ableitung der Sinusfunktion des Flußdichteverlaufs und 2-½ ist der Umrechnungsfaktor vom Spitzenwert der Flußdichte in den Effektivwert.
Der Faktor 10000 im Zähler ist für die Umrechnung der Quadratzentimeter Eisenquerschnittsfläche QFe in Quadratmeter.
Die Spannungserzeugungsformel dient zur praktischen Berechnung von Transformatoren. Sie bezieht sich auf Spitzenwerte der magnetischen Flußdichte.
Anhand dieser Formel wird auch schnell klar warum Transformatoren für niedrige Frequenzen (z.B. bei der Bahn mit 16 ![]() Hz) bei gleicher Flußdichte größer sind als die für hohe Frequenzen.
Hz) bei gleicher Flußdichte größer sind als die für hohe Frequenzen.
Siehe auch:
» Transformator » Magnetische Flußdichte » Bemessungsspannung » Übersetzungsverhältnis » Induktionsgesetz » Magnetische Verkettung ΨSpartransformator
Ein Spartransformator unterscheidet sich von anderen Transformatoren dadurch, daß Primär- und Sekundärseite nicht galvanisch getrennt sind.
Beide Spannungen werden an einer Wicklung angelegt bzw. abgegriffen. Ein Anschluß am Ende jeder Wicklung ist für beide Seiten gemeinsam. Ein zweiter Anschluß befindet sich irgendwo zwischen Anfang und Ende der Wicklung. Der dritte Anschluß am anderen Ende der Wicklung kann ebenso wie der zweite entweder der Primär- oder der Sekundärseite zugeordnet werden, je nachdem ob die Spannung hoch oder runter transformiert werden soll.
Durch diese Bauweise spart man die Isolation zwischen Primär- und Sekundärseite.
Die beiden Seiten sind also sowohl elektrisch als auch magnetisch verkoppelt. Das bedeutet, daß sie sich wie ein induktiver Spannungsteiler verhalten, was nach der Spannungserzeugungsformel nicht im Wiederspruch zur magnetischen Verbindung der beiden Wicklungen steht.
Im Unterschied zu einem Spannungsteiler aus zwei Induktivitäten, die nicht magnetisch verbunden sind, kann mit dieser Schaltung eine Eingangspannung auch "aufwärts" geteilt werden.
D.h. man legt an einer Teilwicklung eine Eingangspannung an und entnimmt der Gesamtwicklung eine größere Ausgangsspannung.
Am besten verhält sich ein solcher Transformator wenn primäre und sekundäre Bemessungsspannung dicht beieinander liegen, weil dann das geringste Streufeld ensteht, und weil ein Großteil des Stroms direkt durch den kleineren der beiden Wicklungsabschnitte auf die Sekundärseite fließt.
Bezüglich der vorgegebenen Stromstärke wird der Spartransformator oft so ausgelegt, daß verschiedene Leiterquerschnitte gewählt werden, von denen einer für den Bemessungstrom der Oberspannungsseite ausgelegt ist, und der andere für die Differenz aus dem Bemessungstrom der Unterspannungsseite und dem der Oberspannungsseite.
Daher werden z.B. wenn das Übersetzungsverhältnis nahe bei 1 liegt, verschiedene Leiterquerschnitte miteinander verlötet.
Anwendungsgebiete des S. sind z.B. das Anlassen von großen Asynchronmotoren, die dann durch die reduzierte Eingangspannung einen viel geringeren Einschaltstrom brauchen. Haben sie eine gewisse Drehzahl erreicht, wird von der reduzierten Spannung am Ausgang des S. auf die volle Spannung umgeschaltet.
Allgemein sind Spartransformatoren gut geeignet, wenn es um das Verstellen einer Spannung ohne großen Energieverlust geht.
Siehe auch:
» Primär- und Sekundärseite » Spannungserzeugungsformel » Induktivität » StreufeldStrangspannung und -Strom
Als einen Strang kann man jede Strecke der Leiter eines Transformators zwischen zwei möglichst nahe beieinander liegenden, verschiedenen Punkten bezeichnen, welche beide die Eigenschaft haben in Bezug auf den Stromkreis ein Knotenpunkt zu sein oder direkt (d.h. nicht über eine Leitungsstrecke) mit einem der Außenleiter verbunden zu sein.
Daraus folgt, daß man aus drei Außenleitern, mit drei Leitungsstrecken, die drei Stränge bilden zwei punktsymmetrische Schaltungen aufbauen kann.
Das sind Stern- und Dreieckschaltung, die zum Aufbau unterschiedlicher Schaltgruppen dienen. Eine Besonderheit stellt die z- Schaltung dar, die aus sechs Leitungsstrecken besteht, die jeweils in zweier Gruppen zu einem Strang verschaltet werden.
Das oben mehrmals verwendete Wort "Leitungsstrecke" meint dabei den größtmöglichen Leiterabschnitt, der sich aus Wicklungen um einen einzelnen Schenkel des Kerns zusammensetzt und in seinem inneren Knotenpunktsfrei ist oder aus Leitungsstrecken, die in ihrem inneren jeweils knotenpunktsfrei sind, zusammengesetzt ist.
Die Strangspannung ist die Spannung, die zwischen den Enden eines Strangs herrscht; der Strangstrom ist der Strom, der zwischen den Endpunkten eines Strangs fließt.
Die Umrechnung der Strangspannung und des Strangstroms in Außenleiterwerte in Abhängigkeit von der Schaltung ist bei dem Eintrag Schaltgruppen beschrieben.
Siehe auch:
» Transformator » Kern » Außenleiterspannung, -stromStreufeld
Das Streufeld ist der Anteil des magnetischen Flusses, der an dem von dem Konstrukteur einer elektrischen Maschine vorgegebenen Weg vorbei, durch die Luft oder andere Maschinenteile fließt. Weil der magnetische Widerstand des verwendeten Werkstoffs nicht beliebig klein sein kann und und auch die Umgebungsluft eine Permeabilität µ0 hat läßt sich ein gewisses Streufeld nie ganz vermeiden.
In einem gewissen Zusammenhang ist das Streufeld beim Transformatorenbau jedoch nützlich, weil es den Effekt einer in Reihe geschalteten Induktivität ohne zusätzliche Bauteile erzielt. Dadurch läßt sich der Kurzschlußstrom und der Einschaltstrom begrenzen, was zu einer Eigensicherheit des Trafos durch die entsprechende Kurzschlußfestigkeit führen kann.
Gemäß Ersatzschaltbild muß man das Streufeld in zwei Anteile aufteilen:
Einen belastungsabhängigen Teil, der durch die Streuinduktivitäten verursacht wird. Und einen Anteil, der aus dem magnetischen Hauptfluß ensteht, wenn dieser an den Ecken des Kerns ausbricht.
Den Umfang dieses Anteils kann man nicht von außen durch Meßwerte an den elektrischen Anschlüssen ermitteln. Man müsste mit einem B - Feld-Sensor Messungen des Magnetfeldes in der Nähe des Kerns durchführen.
Oft bezieht man sich mit dem Begriff "Streufeld" nur auf den lastabhängigen Teil, weil der Streufluß der Hauptinduktivität schon bei geringer Belastung des Transformators viel kleiner ist.
Außerdem deutet der Name "Streuinduktivität" schon an, daß der Streufluß, der magnetische Fluß ist, der zur Streuinduktivität gehört.
Problematisch wird das Streufeld z.B. dann, wenn es Wirbelströme in das Gehäuse des Transformators induziert und dort ohmsche Verluste erzeugt.
Außerdem steigt durch einen größeres Streufeld infolge eines hohen magnetischen Widerstands des Kerns der Leerlaufstrom an und der Wirkungsgrad des Transformators nimmt ab, wenn die Feldlinien des Streufelds, wo sie aus dem Kern ausbrechen, nicht in der Vorzugsrichtung des magnetischen Werkstoffs liegen.
Meistens ist die Aufgabe also das Belastungsabhängige Streufeld richtig zu dosieren und auf den richtigen Wegen zu leiten (z.B. im Streukanal zwischen Primär- und Sekundärwicklung) und das Streufeld, das durch die Hauptinduktivität erzeugt wird, so gering wie möglich zu halten.
Siehe auch:
» Magnetischer Fluß Φ » Magnetische Widerstand Rm » Permeabilität » Induktivität » Kurzschlußstrom » Einschaltstrom » Kurzschlußfestigkeit » Wirbelstromverluste » Zusatzverluste » Leerlaufstrom » Feldlinien » VorzugsrichtungStromverdrängung
Als Stromverdrängung oder Skineffekt bezeichnet man das Ansteigen des ohmschen Widerstands bei Wechselstrom mit zunehmender Frequenz und mit steigendem Leiterquerschnitt gegenüber dem Gleichstromwiderstand. Dies ist darauf zurückzuführen, daß das durch den fließenden Strom selbst verursachte, ständig wechselnde B - Feld innerhalb des Leiters ein elektrisches Feld induziert, das die Leitungselektronen an den Rand des Leiters drängt.
Dadurch wird nicht der ganze Leiterquerschnitt voll genutzt, der Spannungsabfall pro Meter, also der ohmsche Widerstand des Leiters steigt an.
Die Stärke der Widerstandssteigerung ist nicht vom fließenden Strom, sondern nur von Frequenz, Querschnittsfläche, Form des Querschnitts, Permeabilität und spezifischem Leitwert abhängig.
Wenn man den Strom über mehrere getrennte Leiter transportiert kann man die Stromverdrängung vermindern. Material sparen kann man bei der Hochfrequenztechnik durch hohle Leiter, weil man die Bereiche, die sowieso wenig Strom führen wegläßt.
Bei einer Netzfrequenz von 50 Hz ist die Stromverdrängung schon bei Einzelleitern von einigen 100 mm2, wie sie in Folienwicklungen von Hochstromtransformatoren vorkommen, deutlich messbar.
Beim Trafobau sind neben der Stromverdrängung die Wirbelstromverluste der wichtigste Grund, warum man Leiter aufteilt.
Siehe auch:
» Magnetische Flußdichte » Stromverdrängung » WirbelstromverlusteStromwandler und Spannungswandler
Stromwandler und Spannungswandler sind Spezialformen von Transformatoren, die durch das vorhandene Übersetzungsverhältnis große Wechselspannungen und -ströme in einen leichter meßbaren Bereich heruntertransformieren und außerdem die Meßeinrichtungen galvanisch von dem zu messenden System trennen.
Sie werden ausschließlich zum Messen oder Regeln benutzt, die Übertragung großer Leistungen ist nicht ihre Aufgabe. Daher werden sie auch "Meßwandler" genannt.
Stromwandler werden in Reihe in einen Strang geschaltet und transformieren Ströme entsprechend ihres Windungszahlverhältnisses herab ( I1 / N2 = I2 / N1 ) . Sie müssen am Ausgang mit einem kleinen Widerstand belastet werden, sonst kann die Spannung dort auf sehr hohe Werte ansteigen. Oft wird an den Ausgang eines Stromwandlers ein Strommeßgerät geschaltet, das die Bedingung einer niedrigen Eingangsimpedanz erfüllt.
Spannungswandler sind in der Hinsicht unproblematischer, weil sie im allgemeinen sowohl einen Kurzschluß am Ausgang vertragen als auch den hohen Eingangswiderstand eines Spannungsmessers, für den sie konstruiert wurden.
Bei der Konstruktion von Stromwandlern und Spannungswandlern wird auf ein möglichst gutes Übertragungsverhalten (sehr schmale Hysteresekurve, geringes Streufeld) Rücksicht genommen.
Siehe auch:
» Transformator » Übersetzungsverhältnis » Hysteresekurve » StreufeldTransformator
1. Was ist ein Transformator?
Ein Transformator ist eine Maschine, die mittels magnetischer Induktion eine Eingangspannung in eine Ausgangspannung transformiert.
Diese Aufgabe erfüllt er, ohne daß dazu bewegte Bauteile nötig sind. Das ist ein Grund dafür, daß er für eine hohe Lebensdauer von 25 Jahren konstruiert werden kann.
Magnetische Induktion läßt sich nur im wechselnden Magnetfeld zur Spannungserzeugung anwenden. Daher kann ein Transformator nur mit Wechselstrom funktionieren.
Der Transformator hat eine Primär- und eine Sekundärseite, die jeweils über eine ihrer Bemessungsspannung entsprechenden Anzahl an Windungen mit dem magnetischen Fluß durch seinen Kern verkettet sind.
Die Windungen auf jeder Seite bilden Wicklungen, die meistens nicht elektrisch miteinander verbunden sind (Ausnahme: Spartransformator). Die Verbindung wird also nur durch die oben beschriebene Induktion hergestellt. Dadurch kann der Transformator Energie übertragen.
Da ein T. keine Energie erzeugt muß auf beiden Seiten das Produkt von Spannungen und Strömen, die zueinander in Phase liegen (die Wirkleistung) gleich groß sein (unter Vernachlässigung der Verluste). Diese Einschränkung wird durch die folgenden Formeln zur Übertragung von Spannungen und Strömen erfüllt:
Übertragung von Spannungen und Strömen
Formel T.1: Übertragung von Spannungen und Strömen
Ein Transformator ist also für Spannungen und Ströme das, was ein Getriebe für Kräfte und Drehzahlen ist.
Wobei man folgende Vergleiche anstellen kann:
| Getriebe | Transformator |
|---|---|
| Anzahl der Zähne der Zahnräder eines Zahnradpaares | Anzahl der Windungen auf Primär- und Sekundärseite |
| Verhältnis der Drehmomente | Verhältnis der Spannungen |
| Drehzahlverhältnis | Verhältnis der Ströme |
Aufgrund dieser Analogien ist es sinnvoll auch für den Transformator den Begriff Übersetzungsverhältnis einzuführen.
2. Wozu werden Transformatoren benötigt?
Das Haupteinsatzgebiet für Transformatoren ist die Übertragung von elektrischer Energie von einer Quelle (z.B. Kraftwerk) zu ihrem Einsatzort (Verbraucher) mit möglichst geringen Verlusten.
Für eine wirtschaftlich effiziente Energieübertragung benötigt man nämlich hohe Spannungen, um die ohmschen Verluste gering zu halten.
Wirkungsgrad einer Leitung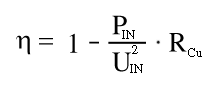
Formel T.2: Wirkungsgrad einer Leitungsstrecke für die Energieübertragung in Abhängigkeit von der Eingangsspannung
Bei dem Verbraucher muß die Spannung dann wieder heruntertransformiert werden, weil der Isolationsaufwand dort sonst zu hoch wäre.
Neben dieser Spannungsanpassung ist ein Transformator auch in der Lage die elektrischen Stromkreise auf Primär und Sekundärseite galvanisch voneinander zu trennen.
Das beruht darauf, daß er nur die Potentialdifferenz an den Anschlüssen der Primärwicklung gemäß seines Windungszahlenverhältnisses überträgt, aber nicht das absolute Potential.
3. Aufteilung der Transformatoren in verschiedene Klassen
Transformatoren lassen sich abhängig von der Betrachtungsweise in verschiedene Gruppen aufteilen.
Dabei kann ein Transformator auch mehreren Gruppen gleichzeitig angehören:
I. Elektrischer Aufbau:
- Spartransformator
- Einphasentransformator
- Drehstromtransformator
- Dreiwicklungs-Transformator
II. Kühlungs- und Isolationsmedien
- Flüssigkeitsgekühlter Transformator (meistens: Öltransformator)
- Gießharztransformator
- Trockentransformator
- Aufteilung nach Isolierstoffklasse
III. Verwendungszweck:
- Hochstromtransformator
- Meßwandler:
- Stromwandler (z.B. Zangenamperemeter)
- Spannungswandler
- Impedanzwandler
- Netztransformator
- Schweißtransformator
- Stelltransformator
- Trenntransformator
IV. Bauweise
- Form des Kerns:
- Bei Drehstromtransformatoren:
- Fünfschenkelkerntransformator
- Dreischenkelkerntransformator
- Ringkerntrafo
- Schnittbandkerntrafo
- Stufenkerntrafo
- Einphasen- Kerntransformator
- Einphasen- Mantelkerntransformator
- Bei Drehstromtransformatoren:
- Stelltransformatoren:
- Thomaregler
- Drehtransformator
- Transformator mit Stufenschalter
V. Spezialformen:
- Teslatransformator
- Schleppkabelstation
- Funkeninduktor
4. Das Funktionsprinzip im Detail
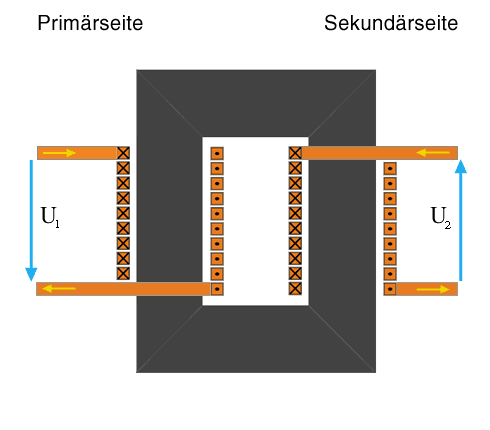
Bild K.4: Einphasentransformator mit Wicklungen im Schnitt und Stromflußrichtungen
Wie man aus der obigen Abbildung entnehmen kann erzeugen Primär- und Sekundärwicklung Felder in unterschiedliche Richtungen. Das beruht auf der Lenzschen Regel.
Aus dem Durchflutungssatz läßt sich folgern, daß die magnetische Durchflutung entlang des Kerns 0 ist und er daher kein Feld enthält.
Aber das stimmt nicht ganz, weil die von der Primärseite erzeugte Durchflutung aufgrund des Leerlaufstroms doch geringfügig höher ist als die auf der Sekundärseite.
Spannungen und Ströme werden nach Formel T.1 entsprechend des Windungszahlenverhältnisses übertragen, was auf die Verkettung der magnetischen Wirkung durch elektrische Reihenschaltung zurückzuführen ist.
5. Grundlagen der technischen Realisierung
Unter den gegebenen Voraussetzungen nimmt ein T. die Gestalt an, die er heute hat:
- Stromleiter, die meist als zylinderförmige Wicklungen geformt werden und das Magnetfeld erzeugen und aufnehmen. Die Leiter jeder Wicklung sind über das Magnetfeld, das den Kern durchflutet verkoppelt. Meistens sind die Wicklungen konzentrisch um den Kern angeordnet.
- Einen Kern, der die Stromleiter umschließt, sowie auch die Leiter den Kern umschließen.
- Kern und Leiter sind aus Werkstoffen, die ihrem Verwendungszweck am ehesten gerecht werden (d.h. der Kern aus kornorientierten Trafoblechen und die Leiter aus Kupfer).
- Der Kern ist aus fertigungstechnischen Gründen oft eckig, folgt also nicht exakt dem Verlauf der Feldlinien. Die Drähte sind, weil sie aus dem flexiblen Metall Kupfer bestehen meistens kreisförmig um den Kern gewickelt (es gibt für kleine Leistungen auch rechteckige Spulen)
Wenn man den Transformator nicht als Blackbox betrachten will, sondern seine Rückwirkungen auf elektrische Netzwerke berücksichtigen muß, ist das Ersatzschaltbild das richtige Hilfsmittel.
6. Einige Fragen zum Thema Transformator
Warum sind in einem Transformator nur ganzzahlige Windungszahlen möglich?
Bei der Betrachtung eines Transformators darf man den Stromkreis nicht nur als Fluß zwischen zwei Punkten sehen, sonden man muß sich auf die gesamte geschlossene Leiterschleife beziehen.
Dann wird klar, daß man keine halben Leiterschleifen bilden kann, ohne den Kern zu durchbohren und den Leiter hindurch zu führen, was einen viel zu großen Aufwand bedeutet. Der Stromkreis kann den Kern sonst nämlich nur ganz umschließen, oder er kommt bloß in seine Nähe und erzeugt nur ein geringes lokales Streufeld im Eisen des Kerns.
Weil in bezug auf eine einzelne Windung nur die Abstufungen 0 oder 1 möglich sind, kann eine Wicklung unter dem Aspekt der magnetischen Verkopplung des Kerns mit dem Gesamtstromkreis nur aus einer ganzzahligen Anzahl von Windungen bestehen.
Bei einem Thomaregler wird diese Einschränkung letztlich durch das oben beschriebene Durchqueren des Kerns mit einem Leiter umgangen.
Warum sind die Eisenverluste nicht belastungsabhängig?
Das Magnetfeld im Kern nimmt mit steigender Belastung des Transformators nicht zu, weil der Strom in der Sekundärwicklung durch Induktion ein Gegenfeld zu dem belastungsabhängigen Strom auf der Primärseite aufbaut.
Daher wird wie oben beschrieben immer nur das Feld des Leerlaufstroms mit den entsprechenden Verlusten im Kern erzeugt.
Wieso sind kleine Transformatoren verhältnismäßig groß und schwer?
Kleinere Transformatoren erwecken häufig den Eindruck, daß sie für die geringe Leistung, die sie übertragen, zuviel Raum und Gewicht in Anspruch nehmen. Mit zunehmender Leistung steigt das Gewicht nämlich nicht linear sondern etwa mit ![]() , was dazu führt, das größere Transformatoren mehr Leistung pro Kilogramm bringen. Diese Gesetzmäßigkeit hängt damit zusammen, daß die Leistung eines Tranformators einerseits linear mit der Eisenquerschnittsfläche und andererseits linear mit dem Kupferquerschnitt zusammenhängt.
, was dazu führt, das größere Transformatoren mehr Leistung pro Kilogramm bringen. Diese Gesetzmäßigkeit hängt damit zusammen, daß die Leistung eines Tranformators einerseits linear mit der Eisenquerschnittsfläche und andererseits linear mit dem Kupferquerschnitt zusammenhängt.
Bei Betrachtung des Leistungsanstiegs im Verhältnis zu einer einzelnen Größe (Kupferquerschnitt oder Eisenquerschnitt) kommt jeweils heraus, daß die Leistung stärker als das Gewicht, nämlich mit dem Faktor ![]() ansteigt.
ansteigt.
Das ergibt sich daraus, das sowohl die Umfangslänge des Kerns, als auch die der Wicklungen nicht linear mit der jeweils anderen Querschnittsfläche steigt.
Dann müßte man Transformatoren möglichst groß bauen. Gibt es dafür eine obere Grenze?
Das Problem bei Transformatoren ist, daß sie mit zunehmender Größe ihre Abwärme immer schlechter loswerden, weil die Oberfläche im Gegensatz zur Verlustleistung nicht linear mit dem Volumen steigt.
Einerseits müssen sie kompakt sein um geringe Verluste zu erzeugen und andererseits hindert ihre kompakte Bauform sie daran, die Abwärme abzugeben.
Daraus folgt, daß es eine Wirtschaftlichkeitsgrenze gibt, ab der man keine größeren Transformatoren mehr bauen sollte.
Warum verzichtet man nicht einfach auf den Eisenkern, wo er doch nur Verluste erzeugt?
Um den Leerlaufstrom klein zu halten müßte der Transformator dann aus vielen sehr großen Drahtschleifen bestehen, die wiederum beträchtliche ohmsche Verluste erzeugen. Es könnte jedoch sein, daß die Leerlaufverluste etwas geringer ausfallen.
In jedem Fall würde ein solcher Transformator ein Streufeld, das nicht aktzeptabel ist, in die Umgebung abgeben. Der Eisenkern wird also benötigt um möglichst kompakt den Raum um die Wicklungen herum zu überbrücken.
Kann man das Funktionsprinzip eines Transformators auch in der Hinsicht umkehren, daß man den Kern jeweils in mehreren Windungen um eine einzelne Leiterwicklung auf jeder Seite wickelt?
Ja, das geht.
Die Wicklungen bestehen dann aus Eisen, statt aus Kupfer, wodurch sie sehr schwer zu verarbeiten sind.
Siehe auch:
» Induktion » Primär- und Sekundärseite » Bemessungsspannung » Magnetischer Fluß Φ » Kern » Magnetische Verkettung Ψ » Wirkleistung » Verluste » Übersetzungsverhältnis » Spartransformator » Drehstromtransformator » Isolierstoffklassen » Stromwandler und Spannungswandler » Lenzsche Regel » Magnetische Durchflutung Θ » Durchflutungssatz » Leerlaufstrom » FeldlinienÜbersetzungsverhältnis
Das Übersetzungsverhältnis ü wird je nach Verwendungszweck mit sehr verschiedenen Bedeutungen wiedergegeben:
- Komplexes Übersetzungsverhältnis:
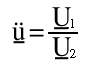
Formel U.1: Komplexes Übersetzungsverhältnis als Verhältnis der Bemessungsspannungen
Dieses Ü. ist das Verhältnis der komplexen Bemessungsspannungen und gibt daher die Phasenverschiebung im Leerlauf gut wieder. Es eignet sich für die Charakterisierung von Schaltgruppen. Natürlich ändert sich diese Phasenverschiebung unter Belastung, was durch dieses Ü. nicht mit erfasst wird. - Übersetzungsverhältnis aus dem Windungszahlenverhältnis für das Ersatzschaltbild
Für das Ersatzschaltbild braucht man ein Übersetzungsverhältnis, das nicht durch die Eigenschaften der Bauelemente des Ersatzschaltbilds beeinflußt wird, weil die ja schon vorgegeben sind. Für seine Bestimmung und Anwendung ist, wenn hohe Genauigkeit erwünscht ist, ein Ü. das aus dem Windungszahlenverhältnis N1 / N2 bestimmt wird, erforderlich: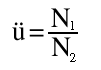
Formel U.2: Reeles Übersetzungsverhältnis als Verhältnis der Windungszahlen
So kann man die Phasenverschiebung und das Spannungsverhältnis bei jedem Belastungszustand über das Ersatzschaltbild bestimmen. - Andere Übersetzungsverhältnisse, die im Ersatzschaltbild verwendet werden:
Wenn man das Ersatzschaltbild entsprechend anpaßt kann man ü fast beliebig wählen. Das ändert jedoch nichts daran, daß man für eine genaue Berechnung Informationen über das Windungszahlenverhältnis braucht. Wenn man ü von den Windungszahlen unabhängig macht, muß man Bauteilgrößen kennen, die man nur aus dem Windungszahlenverhältnis bestimmen kann.
Siehe auch:
» BemessungsspannungVerluste
Transformatoren geben die Energie, die man auf der Primärseite hineinsteckt auf der Sekundärseite nicht zu 100% zurück. Den Anteil, der fehlt bezeichnet man als Verlustleistung.
Wie bei den meisten elektrischen Maschinen teilen sich die Verluste bei Transformatoren in folgende Gruppen auf:
- Kupferverluste
- Wirbelstromverluste
- Hystereseverluste
Wirbelstromverluste im Eisen des Kerns und Hystereseverluste werden zusammen als Eisenverluste bezeichnet. Außerdem gibt es die Zusatzverluste, die meist nur einen geringen Anteil haben.
Diese Aufteilung entspricht teilweise (Wirbelstromverluste, Hystereseverluste) den möglichen Ursachen für Verluste, teilweise sind die Bezeichnungen durch das Bauteil geprägt, in dem die Verluste enstehen (Kupferverluste, Eisenverluste).
Beim Transformator treten die Verluste durch einige Ursachen also nur an bestimmten Stellen auf. Deshalb fließt die Trennung nach Verlustursache mit der Trennung nach Ort der Verlustleistung teilweise zusammen.
Und dann gibt es noch eine Unterscheidung der Verluste als äußere elektrische Meßwerte nach dem Belastungszustand des Transformators, bei dem sie bestimmt werden.
Weil durch die Verlustleistung wertvolle elektrische Energie in nutzlose oder sogar schädliche Wärmeenergie umgesetzt wird ist die Reduzierung der Verluste bei der Konstruktion von Transformatoren ein wichtiges Ziel. Hierzu werden optimierte magnetische Werkstoffe eingesetzt, und die richtige Dimensionierung aller Bauteile beachtet.
Siehe auch:
» Kupferverluste » Wirbelstromverluste » Hystereseverluste » Eisenverluste » Zusatzverluste » Kurzschlußverluste » LeerlaufverlusteVorzugsrichtung
Die Vorzugsrichtung ist ein Phänomen, daß z.B. bei kaltgewalzten, kornorientierten Trafoblechen auftritt.
Die Permeabilität des Materials ist dann abhängig von der Richtung der Feldlinien. Wenn sich die Richtung gegenüber der Vorzugsrichtung ändert, fällt die Permeabilität stark ab und ist schlechter als bei einem Werkstoff, der keine V. hat. Die Eisenverluste sind dann oft höher als bei Stoffen ohne Vorzugsrichtung.
In Vorzugsrichtung ist die Permeabilität so hoch und die Verluste sind so gering, daß sich die Verwendung von kornorientierten Blechen lohnt.
Magnetische Werkstoffe haben überwiegend eine symmetrische Hysteresekurve. Deshalb ist die Vorzugsrichtung eine Achse und nicht ein einzelner Richtungspfeil.
D.h. wenn in einer Bestimmten Richtung der magnetischen Erregung eine bestimmte Permeabilität herrscht, gibt es im Winkel von 180° dazu die selbe Permeabilität.
Siehe auch:
» Feldlinien » Permeabilität » Eisenverluste » Bleche » Hysteresekurve » Magnetische Erregung HWirbelstromverluste
Wirbelstromverluste entstehen immer, wenn es in einem elektrisch leitfähigen Material zu einer Veränderung der Flußdichte B kommt. Je stärker diese Veränderung bezüglich der Zeit ist, umso größer ist die induzierte Spannung ( Induktionsgesetz ).
Weil die in Wärme umgesetzte Leistung nach dem ohmschen Gesetz im Quadrat zur Spannung steigt und die Stärke der Veränderung des Flusses Φ sich linear zur Frequenz verhält steigen die Wirbelstromverluste quadratisch mit der Frequenz an. Das unterscheidet sie von den Hystereseverlusten , die linear mit der Frequenz ansteigen. Mit der Feldstärke wachsen die W. ebenfalls quadratisch.
Die Wirbelstromverluste im Kern eines Transformators, die zu den Eisenverlusten gezählt werden, werden durch die Aufteilung in dünne Trafobleche gering gehalten.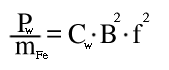
Formel W.1: Wirbelstromverluste im Kern des Transformators in Abhängigkeit von Flußdichte und Frequenz
Die Konstante Cw läßt sich nicht rechnerisch bestimmen sondern muß aus den Angaben des Herstellers der Trafobleche hergeleitet werden.
Bei den Zusatzverlusten handelt es sich ebenfalls größtenteils um Wirbelstromverluste und die Kupferverluste enthalten auch einen Anteil an W.
Dieser Anteil der Kupferverluste, der durch das Streufeld verursacht wird, wenn es die Wicklungen durchdringt, kann durch die Verwendung mehrerer paraleller Leiter minimiert werden.
Siehe auch:
» Magnetische Flußdichte » Induktionsgesetz » Hystereseverluste » Eisenverluste » KupferverlusteWirkleistung
Die Wirkleistung wird mit dem Buchstaben P bezeichnet und in Watt (W) gemessen. In vektorieller Darstellung bilden Blindleistung, Wirkleistung und Scheinleistung als skalare Größen entlang der hier dargestellten Zählpfeile immer ein rechtwinkliges Dreieck.
S-P-Q Dreieck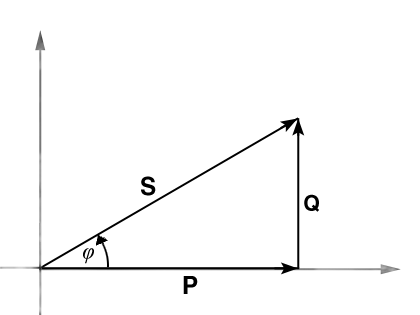
Bild B.1: Das S-P-Q Dreieck![]()
Formel W.2: Die Wirkleistung entspricht der auf die Längsachse projizierten Scheinleistung
Deshalb kann man mit dem Satz des Pythagoras aus zwei dieser Größen die dritte errechnen.
Die W. wird aus dem Produkt von Spannungen und Strömen, die zueinander in Phase liegen, errechnet.
Sie ist ein Maß für die Energie pro Zeiteinheit, die ein elektrisches System (z.B. ein Motor) umsetzt. Sie beschreibt dabei die Wirkung nach außen, also bei dem Motor mechanische Arbeit und Wärme, die er abgibt.
Spannungen und Ströme, die die gleiche Phasenlage haben, ergeben nämlich für jeden beliebigen Zeitabschnitt eine postive Energie, die den Stromkreis verläßt.
Siehe auch:
» Blindleistung » ScheinleistungZusatzverluste
Die Zusatzverluste eines Transformators sind als Bestandteil der Kurzschlußverluste belastungsabhängig.
Sie setzen sich aus folgenden Teilen zusammen:
- Durch das Streufeld verursacht:
- Wirbelstromverluste im Gehäuse des Transformators, die durch das Streufeld verursacht werden.
- Hytereseverluste im Gehäuse, falls es aus Stahl besteht. Sie werden ebenfalls durch das Streufeld (auch das Streufeld der Zuleitungen) verursacht
- Direkte ohmsche Verluste:
Ohmsche Verluste in den Zuleitungen, die natürlich abhängig von der Belastung sind.
Siehe auch:
» Kurzschlußverluste » Streufeld » Wirbelstromverluste » Hystereseverluste